In order to see diffraction the thickness of the film is
100 A
10,000 A
1mm
1cm
The correct Answer is:2
To determine the thickness of the film required to observe diffraction, we need to consider the relationship between the thickness of the film and the wavelength of the light that is incident on it. Here is a step-by-step solution:
1. Understanding Diffraction:
- Diffraction is the bending of light waves around the edges of an obstacle or aperture. It is most noticeable when the size of the obstacle or aperture is comparable to the wavelength of the light.
Hint: Remember that diffraction occurs when the dimensions involved are on the order of the wavelength of light.
2. Wavelength of Light:
- The wavelength of visible light typically ranges from about 400 nm (nanometers) to 700 nm. In angstroms, this translates to approximately 4000 Å (angstroms) to 7000 Å.
Hint: Convert the wavelength of light from nanometers to angstroms for easier comparison with film thickness.
3. Thickness of the Film:
- For diffraction to be observable, the thickness of the film must be comparable to the wavelength of the light. This means that the thickness should be on the order of the wavelength of the light used.
Hint: Think about the relationship between the thickness of the film and the wavelength of the light; they should be of the same order.
4. Conclusion:
- Since the wavelength of visible light is in the range of 4000 Å to 7000 Å, the thickness of the film should also be around this range. For practical purposes, we can say that the thickness of the film should be on the order of 10,000 Å to ensure that diffraction effects are noticeable.
Hint: The thickness of the film should be at least in the range of the visible light wavelengths to observe diffraction clearly.
Final Answer:
The thickness of the film required to see diffraction is approximately 10,000 Å (angstroms).
- Diffraction is the bending of light waves around the edges of an obstacle or aperture. It is most noticeable when the size of the obstacle or aperture is comparable to the wavelength of the light.
- The wavelength of visible light typically ranges from about 400 nm (nanometers) to 700 nm. In angstroms, this translates to approximately 4000 Å (angstroms) to 7000 Å.
- For diffraction to be observable, the thickness of the film must be comparable to the wavelength of the light. This means that the thickness should be on the order of the wavelength of the light used.
- Since the wavelength of visible light is in the range of 4000 Å to 7000 Å, the thickness of the film should also be around this range. For practical purposes, we can say that the thickness of the film should be on the order of 10,000 Å to ensure that diffraction effects are noticeable.
The thickness of the film required to see diffraction is approximately 10,000 Å (angstroms).
Topper's Solved these Questions
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-H
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE
58 Videos
Similar Questions
YDSE is carried out in a liquid of refractive index μ=1.3 and a thin film of air is formed in front of the lower slit as shown in the figure. If a maxima of third order is formed at the origin O, find the thickness of the air film. Find the positions of the fourth maxima. The wavelength of light is air is λ0=0.78μm and D/d=1000.
View SolutionWhen the plastic thin film of refractive index 1.45is placed in the path of one of the interfering waves then the central fringe is displaced through width of five fringes.The thickness of the film will be ,if the wavelength of light is5890Å
View Solution
Knowledge Check
On introducing a thin film in the path of one of the two interfering beam, the central fringe will shift by one fringe width. If μ=1.5, the thickness of the film is (wavelength of monochromatic light is λ)
A4λB3λC2λDλ
White light reflected from a soap film (Refractive index =1.5 ) has a maxima at 600 nm and a minima at 450 nm at with no minimum in between. Then, the thickness of the film is
View SolutionWhite light reflected at normal incidence from a soap film has minima at 6500Å and maxima at 7500Å in the visible region without minimum in between. If μ is 53 for the thin film, thickness of the film is
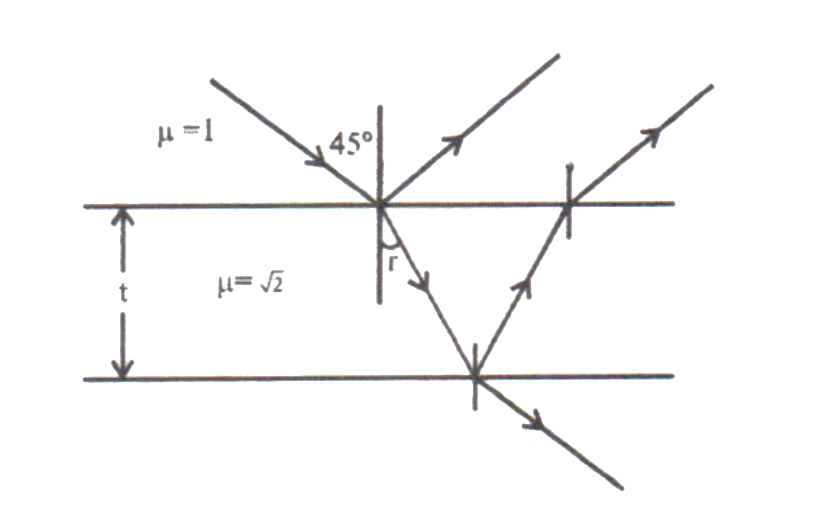
View SolutionA ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
View SolutionIn Fresnel's class of diffraction the
View SolutionA : If a thin soap film is arranged vertically the spectrum of coloured fringes are spread equally on the film.
R : The colours of the film is dependent on the thickness of film and wavelength of the light.
View SolutionA light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
View SolutionFind the minimum thickness of a film which will strongly reflect the light of wavelength 589 nm. The refractive index of the material of the film is 1.25.
View Solution
