Temperature dependent equation can be written as:
Ink=InA−EaRT
Ink=InA+eE2/RT
InK=InA−eRT/Ea
All of these
The correct Answer is:A
To solve the question regarding the temperature-dependent equation, we will derive the Arrhenius equation step by step.
1. Understand the Arrhenius Equation:
The Arrhenius equation describes how the rate constant (k) of a chemical reaction depends on temperature (T). It is given by the formula:
k=Ae−EaRT
where:
- k = rate constant
- A = pre-exponential factor (frequency factor)
- Ea = activation energy
- R = universal gas constant
- T = temperature in Kelvin
2. Take the Natural Logarithm of Both Sides:
To linearize the equation, we take the natural logarithm (ln) of both sides:
lnk=lnA+ln(e−EaRT)
Using the property of logarithms that states ln(ex)=x, we can simplify this further.
3. Simplify the Equation:
The equation becomes:
lnk=lnA−EaRT
4. Final Form of the Temperature-Dependent Equation:
Thus, the temperature-dependent equation can be expressed as:
lnk=lnA−EaRT
This is the required form of the temperature-dependent equation.
5. Identify the Correct Option:
From the options provided, the correct expression is:
lnk=lnA−EaRT
This corresponds to the first option given in the question.
Conclusion:
The temperature-dependent equation can be written as:
lnk=lnA−EaRT
The Arrhenius equation describes how the rate constant (k) of a chemical reaction depends on temperature (T). It is given by the formula:
k=Ae−EaRT
where:
- k = rate constant
- A = pre-exponential factor (frequency factor)
- Ea = activation energy
- R = universal gas constant
- T = temperature in Kelvin
To linearize the equation, we take the natural logarithm (ln) of both sides:
lnk=lnA+ln(e−EaRT)
Using the property of logarithms that states ln(ex)=x, we can simplify this further.
The equation becomes:
lnk=lnA−EaRT
Thus, the temperature-dependent equation can be expressed as:
lnk=lnA−EaRT
This is the required form of the temperature-dependent equation.
From the options provided, the correct expression is:
lnk=lnA−EaRT
This corresponds to the first option given in the question.
The temperature-dependent equation can be written as:
lnk=lnA−EaRT
Similar Questions
STATEMENT-1 : Solution of the differential equation xdy−ydx=ydy is yex/y=c.
and
STATEMENT-2 : Given differential equation can be re-written as d(xy)=−dyy.View SolutionAt a particular temperature and pressure for a real gas Van der Waal's equation can be written as:
(P+aV2m)(Vm−b)=RT
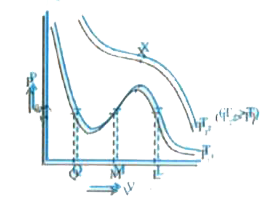
where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L.
As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc.
The expression of Van dcr Waal's constant 'a' can be given asView Solution
Knowledge Check
- Question 1 - Select One
A function in Java can be written
AInside a classBOutside a classCInside main() functionDNone - Question 2 - Select One
The temperature dependence of the rate of a chemical reaction can be explained by Arrhenius equaiton which is
Ak=AeEa/RTBk=Ae−Ea/RTCk=Ae×EaRTDk=Ae×RTEa
For a general electrochemical reaction of the type
αA+bBne−⇐⇒cC+dD
Nernst equation can be written asView SolutionIf reaction between A and B to give C shows first order kinetics in A and second order in B, the rate equation can be written as
View SolutionThe temperature dependence of rate constant (k) of a chemical reaction is written in terms of Arrhenius equation, k=Ae−Ea/RT) Activation energy (Ea) of the reaction can be calculate by plotting
View SolutionTemperature dependence of drift velocity depends on the following factors.
View SolutionAn ideal gas equation can be written as P=ρRTM0 where ρ and M are resp.
View Solution→A+→B can also be written as
View Solution

