Find value of pulling force F for which block just moves. Given coefficient of friction for surface is μ.
The correct Answer is:F=(mug)/(costheta+musintheta)
To find the value of the pulling force F for which the block just moves, we need to analyze the forces acting on the block.
1. Identify the Forces:
- The weight of the block acting downwards: mg (where m is the mass of the block and g is the acceleration due to gravity).
- The normal force N acting upwards.
- The pulling force F applied at an angle θ to the horizontal.
- The frictional force f opposing the motion.
2. Resolve the Pulling Force:
- The horizontal component of the pulling force is Fcosθ.
- The vertical component of the pulling force is Fsinθ.
3. Apply Newton's Second Law in the Vertical Direction:
- The sum of the vertical forces must equal zero for the block to be in equilibrium vertically:
N+Fsinθ=mg
- Rearranging gives:
N=mg−Fsinθ
4. Calculate the Frictional Force:
- The frictional force f is given by:
f=μN
- Substituting for N:
f=μ(mg−Fsinθ)
5. Set Up the Equation for Motion:
- For the block to just start moving, the horizontal component of the pulling force must equal the frictional force:
Fcosθ=f
- Substituting for f:
Fcosθ=μ(mg−Fsinθ)
6. Rearranging the Equation:
- Expanding the right side:
Fcosθ=μmg−μFsinθ
- Bringing all terms involving F to one side:
Fcosθ+μFsinθ=μmg
- Factoring out F:
F(cosθ+μsinθ)=μmg
7. Solve for F:
- Finally, solving for F:
F=μmgcosθ+μsinθ
Final Answer:
The value of the pulling force F for which the block just moves is:
F=μmgcosθ+μsinθ
- The weight of the block acting downwards: mg (where m is the mass of the block and g is the acceleration due to gravity).
- The normal force N acting upwards.
- The pulling force F applied at an angle θ to the horizontal.
- The frictional force f opposing the motion.
- The horizontal component of the pulling force is Fcosθ.
- The vertical component of the pulling force is Fsinθ.
- The sum of the vertical forces must equal zero for the block to be in equilibrium vertically:
N+Fsinθ=mg
- Rearranging gives:
N=mg−Fsinθ
- The frictional force f is given by:
f=μN
- Substituting for N:
f=μ(mg−Fsinθ)
- For the block to just start moving, the horizontal component of the pulling force must equal the frictional force:
Fcosθ=f
- Substituting for f:
Fcosθ=μ(mg−Fsinθ)
- Expanding the right side:
Fcosθ=μmg−μFsinθ
- Bringing all terms involving F to one side:
Fcosθ+μFsinθ=μmg
- Factoring out F:
F(cosθ+μsinθ)=μmg
- Finally, solving for F:
F=μmgcosθ+μsinθ
The value of the pulling force F for which the block just moves is:
F=μmgcosθ+μsinθ
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (WORK POWER & ENERGY)
34 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (CIRCULAR MOTION)
17 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (NEWTONS LAWS OF MOTION)
46 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Find value of pushing force F for which the body just moves.
View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.
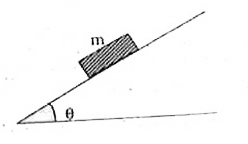
View SolutionIn the given system, a block of mass m is resting on a board which makes an angle θ with the horizontal. What should be the minimum value of θ, so that the block just starts moving downwards? The coefficient of friction between the surfaces of the board and the block is μ.
View SolutionA small object of mass 'm' is moved over a rough, curved surface as shown. The force which moves it along the dotted path shown is always tangential to the curved path. If the object moves with negligible speed, find the work done by the force F in moving it from A to B. The coefficient of friction between the object and the curved surface is μ.

View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
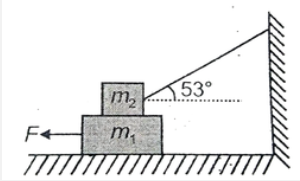
View SolutionCalculate the Force (F) required to cause the block of mass m1=20kg just to slide under the block of mass m2=10kg [ coefficient of friction μ=0⋅25 for all surfaces ]
View SolutionA block of mass m is attached with a massless spring of force constant K. the block is placed over a rough inclined surface for which the coefficient of friction is μ=34 find the minimum value of M required to move the block up the place. (Neglect mass of string and pulley. Ignore friction in pulley).
 .
.
View SolutionA lift moving with a uniform velocity v in which a block of mass m is lying .The friction force offered by the when coefficient of friction is μ=0.5 will be
View SolutionA sufficiently long plane of mass 4kg is placed on a smooth horizontal surfaces A small block of mass 2kg is placed over the plank and is being acted upon by a time varying horizontal force F=(0.5t) where F is in newton and t is in second as shown in figure. The coefficient of friction slipping the plank and the block is given is μs=μk=μ, at time t=12s the relative slipping between the plank and the block is just likely to occur

The coefficient of friction μ is equal to
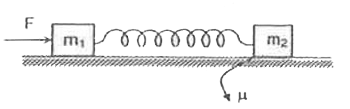
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
View Solution
