Question

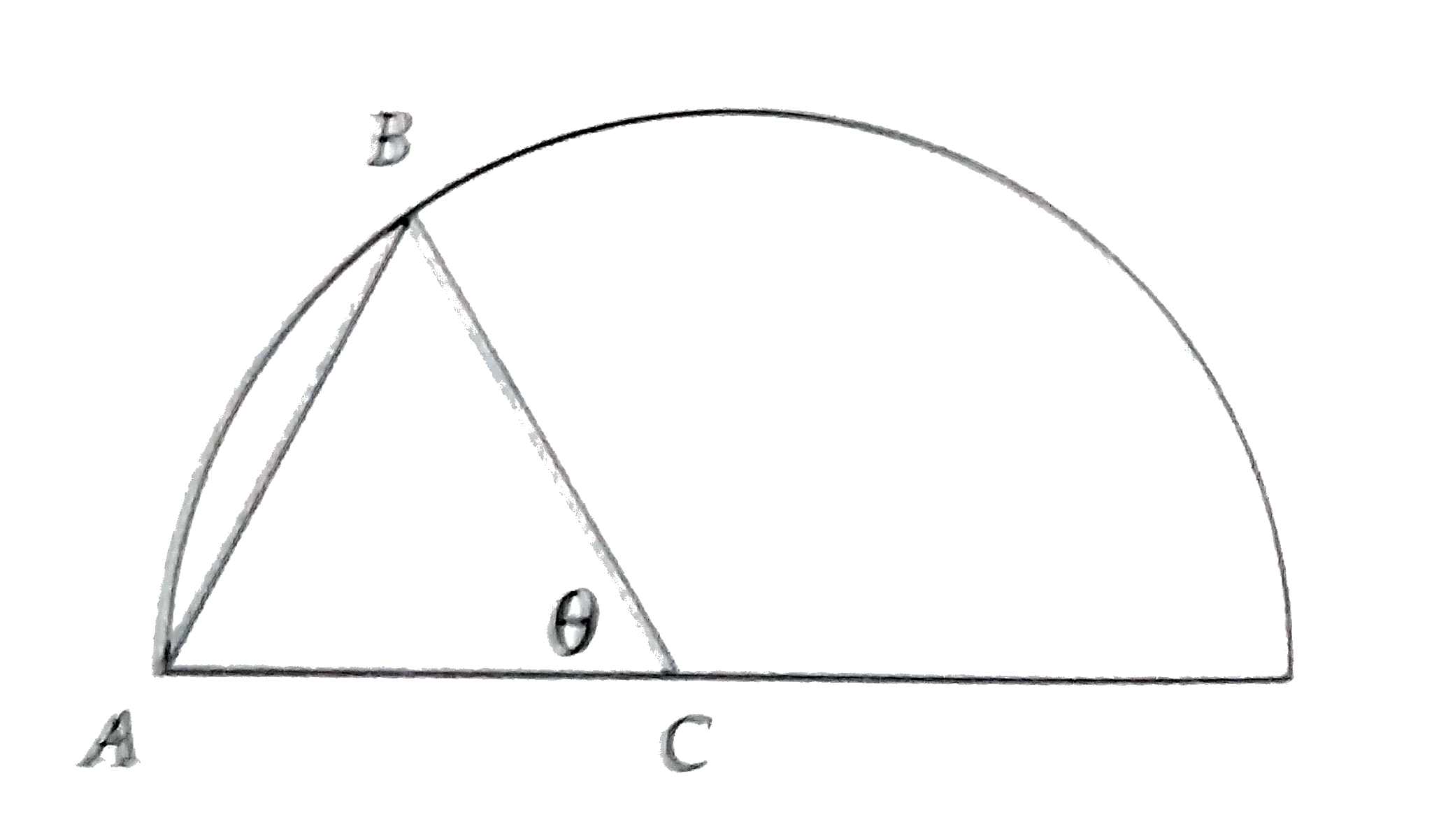
$AB$ is the diameter of a semicircle $k,C$ is an arbitrary point on the semicircle (other than $A$ or $B$) and $S$ is the centre of the circle inscribed into triangle $ABC,$ then measure of-

Options

A. angle ASB changes as C moves on k
B. angle ASB is the same for all positions of C but it cannot be determined without knowing the radius
C. angle `ASB=135^(@)` for all positions of C
D. angle `ASB=150^(@)` for all positions of C

Answer

C

Explanation

To solve the problem, we need to analyze the geometry of the semicircle and the triangle formed by points A, B, and C. Let's break down the solution step by step.

Step 1: Draw the semicircle and label the points
- Draw a semicircle with diameter AB.
- Let A and B be the endpoints of the diameter.
- Choose an arbitrary point C on the semicircle (not equal to A or B).
- Mark the center of the semicircle as O.

Step 2: Identify the angles in triangle ABC
- Since AB is the diameter of the semicircle, by the inscribed angle theorem, we know that angle ACB is a right angle (90 degrees).
- Therefore, we can write:
\( \angle ACB = 90^\circ \)

Step 3: Understand the incenter S
- The point S is the incenter of triangle ABC, which is the point where the angle bisectors of the triangle intersect.
- The angles at A and B can be denoted as:
\( \angle CAB = x \quad \text{and} \quad \angle ABC = y \)
- Since the sum of angles in a triangle is 180 degrees, we have:
\( x + y + 90^\circ = 180^\circ \implies x + y = 90^\circ \)

Step 4: Find angles at S
- The angles at S can be expressed as:
\( \angle SAB = \frac{x}{2} \quad \text{and} \quad \angle SBA = \frac{y}{2} \)
- Therefore, we can write:
\( \angle ASB = 180^\circ - \left(\angle SAB + \angle SBA\right) = 180^\circ - \left(\frac{x}{2} + \frac{y}{2}\right) \)

Step 5: Substitute the values
- Since \( x + y = 90^\circ \), we have:
\( \angle ASB = 180^\circ - \left(\frac{90^\circ}{2}\right) = 180^\circ - 45^\circ = 135^\circ \)

Conclusion
- Therefore, the measure of angle ASB is always 135 degrees, regardless of the position of point C on the semicircle.
- The correct option is:
\( \text{Option C: } \angle ASB = 135^\circ \text{ for all positions of C.} \)