Let A(3,4) and B(5,8)be two points. If C is a point on the x-axis such that AC+BC is minimum then the co ordinates of C are
(5/3 , 0)
(1/3 , 0)
(3,0)
none of these
Clearly , AC + BC , will be minimum when points B , C and D (image of A in x-axis ) are collinear . In that case C is the intersection of BD with x-axis .
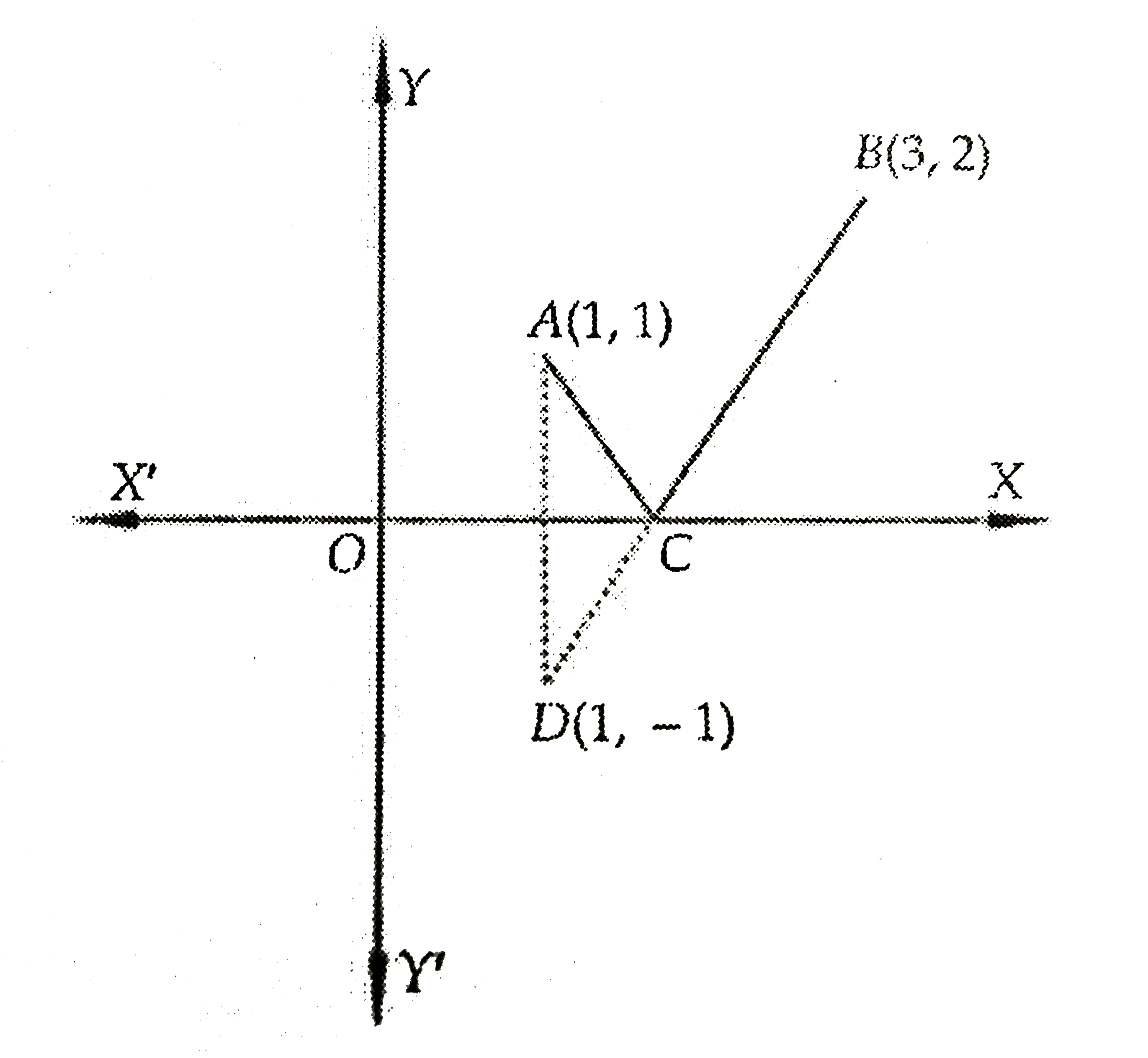
The equation of BD is
y+1=2+13−1(x−1)⇒3x−2y−5=0
It cuts x-axis at (5/3 , 0) .
Hence, the coordinates of the required point are (5/3 , 0)
Topper's Solved these Questions
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Section-1 Solved MCQs (Example)
1 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION - II (ASSERTION - REASON TYPE MCQs)
14 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ILLUSTRATION 18
1 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
Similar Questions
Let A(3, 2) and B(6, 5) be two points and a point C (x,y) is chosen on the line y=x such that AC+BC is minimum, then the co-ordinates of C are:
View SolutionLet A(3, 2) and B(6, 5) be two points and a point C (x,y) is chosen on the line y=x such that AC+BC is minimum, then the co-ordinates of C are:
View SolutionOrdinate of all points on the X-axis is
View SolutionLet A(2,−1,4) and B(0,2,−3) be the points and C be a point on AB produced such that 2AC=3AB, then the coordinates of C are
View SolutionLet A=(a,b) and B=(c,d) where c>a>0 and d>b>0. Then, point C on the X-axis such that AC+BC is the minimum, is:
View SolutionA is a point on x- axis, and point B (5,-4) and AB = 5 units find the co-ordinates of A.
View SolutionIf A(-3,4) ,B(5,6),then find point P on x-axis such that PA+PB is Minimum.
View SolutionA(4,3),B(6,5)andC(5,−2) are the vertices of a ΔABC, if P is a point on BC such that BP:PC=2:3. Find the co-ordinates of P and then prove then ar (ΔABP):ar(ΔACP)=2:3.
View SolutionA point P is reflected in the x-axis. Co-ordinates of its image are (-4, 5).
Find the co-ordinates of P.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
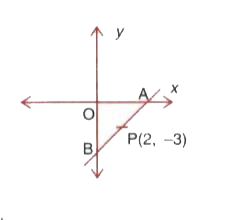
co-ordinates of A and B.
View Solution
