If in a distribution each x is replaced by corresponding value of f(x), then the probability of getting f(x), when the probability of getting xiispi, is.
pi
f(pi)
f(1pi)
none of these
The correct Answer is:A
To solve the problem, we need to understand the relationship between the probabilities of the original values xi and their corresponding transformed values f(xi).
1. Understanding the Given Information:
We are given that the probability of getting xi is pi. This means for each value xi in our distribution, there is a corresponding probability pi.
Hint: Identify what pi represents in the context of the distribution.
2. Replacing xi with f(xi):
The question states that each x is replaced by its corresponding value f(x). Thus, we need to consider the new values f(xi) instead of xi.
Hint: Think about how the transformation f(x) affects the values but not the probabilities.
3. Analyzing the Probability of f(xi):
When we replace xi with f(xi), we need to determine the probability of obtaining f(xi). However, the transformation does not change the underlying favorable cases. The number of favorable outcomes for f(xi) remains the same as that for xi.
Hint: Consider the nature of probability and how it is defined in terms of favorable outcomes.
4. Conclusion:
Since the favorable cases remain unchanged, the probability of getting f(xi) is still pi. Therefore, we conclude that:
P(f(xi))=pi
Hint: Reflect on the principle that the probabilities associated with outcomes do not change when we apply a function to the outcomes.
Final Answer:
The probability of getting f(x) when the probability of getting xi is pi is pi.
We are given that the probability of getting xi is pi. This means for each value xi in our distribution, there is a corresponding probability pi.
The question states that each x is replaced by its corresponding value f(x). Thus, we need to consider the new values f(xi) instead of xi.
When we replace xi with f(xi), we need to determine the probability of obtaining f(xi). However, the transformation does not change the underlying favorable cases. The number of favorable outcomes for f(xi) remains the same as that for xi.
Since the favorable cases remain unchanged, the probability of getting f(xi) is still pi. Therefore, we conclude that:
The probability of getting f(x) when the probability of getting xi is pi is pi.
Topper's Solved these Questions
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section II - Assertion Reason Type
1 Videos
- DETERMINANTSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DETERMINANTSEXERCISE - Chapter Test
30 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - FUNCTIONSEXERCISE - Chapter Test
29 Videos
Similar Questions
When a coin is tossed n times, if the probability for getting 6 heads is equal to the probability of getting 8 heads, then the value of n is
View SolutionSix coins are tossed 6400 times. The probability of getting 6 heads x times using poisson distribution is
View SolutionLet X denote the profit of a business man. The probability of getting profit Rs.3000 is 0.6. The probability of getting loss Rs4000 is 0.3. The probability of getting neither profit nor loss is 0.1 . The mean and variance of X are
View SolutionA random variable X has the following probability distribution :

determine the value of a
View SolutionIn a probability distribution of a random variable X , the sum of probabilities is always
View SolutionThe probability distribution of a discreate random variable X is given below :

The value of k is
View SolutionFor the following probability distribution.
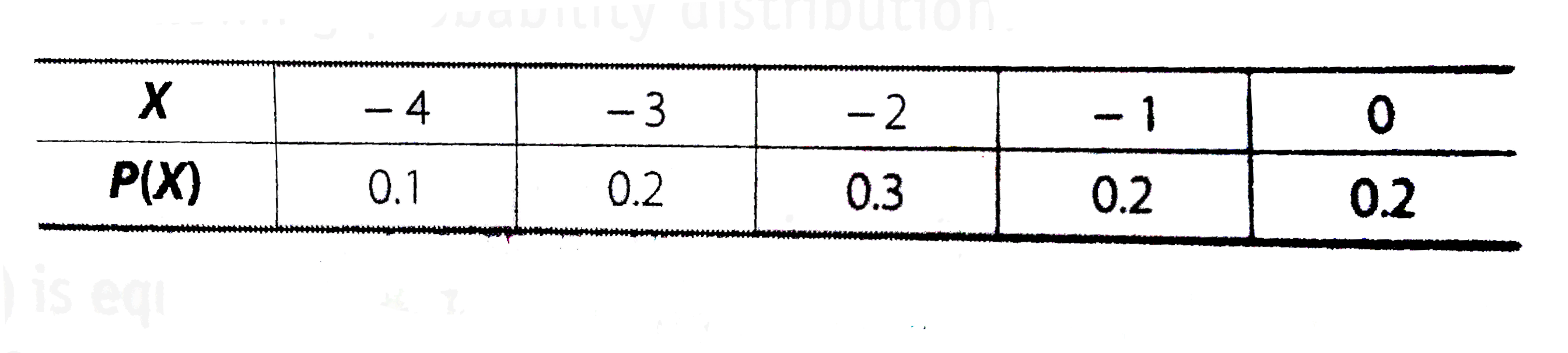
E(X) is equal to
View SolutionA random variable X follows binomial probability distribution with probability P(X), with mean as 2, probability of success as p and probability of failure as q such that p+q=1. If ΣX2P(X)=285, then the probability of exactly 2 success is
View SolutionIf each of n numbers xi=i, is replaced by (i+1)xi, then the new mean is
View SolutionThe probability distribution of a discrete random variable X is given below

The value of k is
View Solution
