The graph of f(x)=x2 and g(x)=cx3 intersect at two points, If the area of the region over the interval [0,1c] is equal to 23, then the value of (1c+1c2) is
20
2
6
12
The correct Answer is:c
The two curves intersect at A(1c,1c2) and O (0,0) as shown in 33.
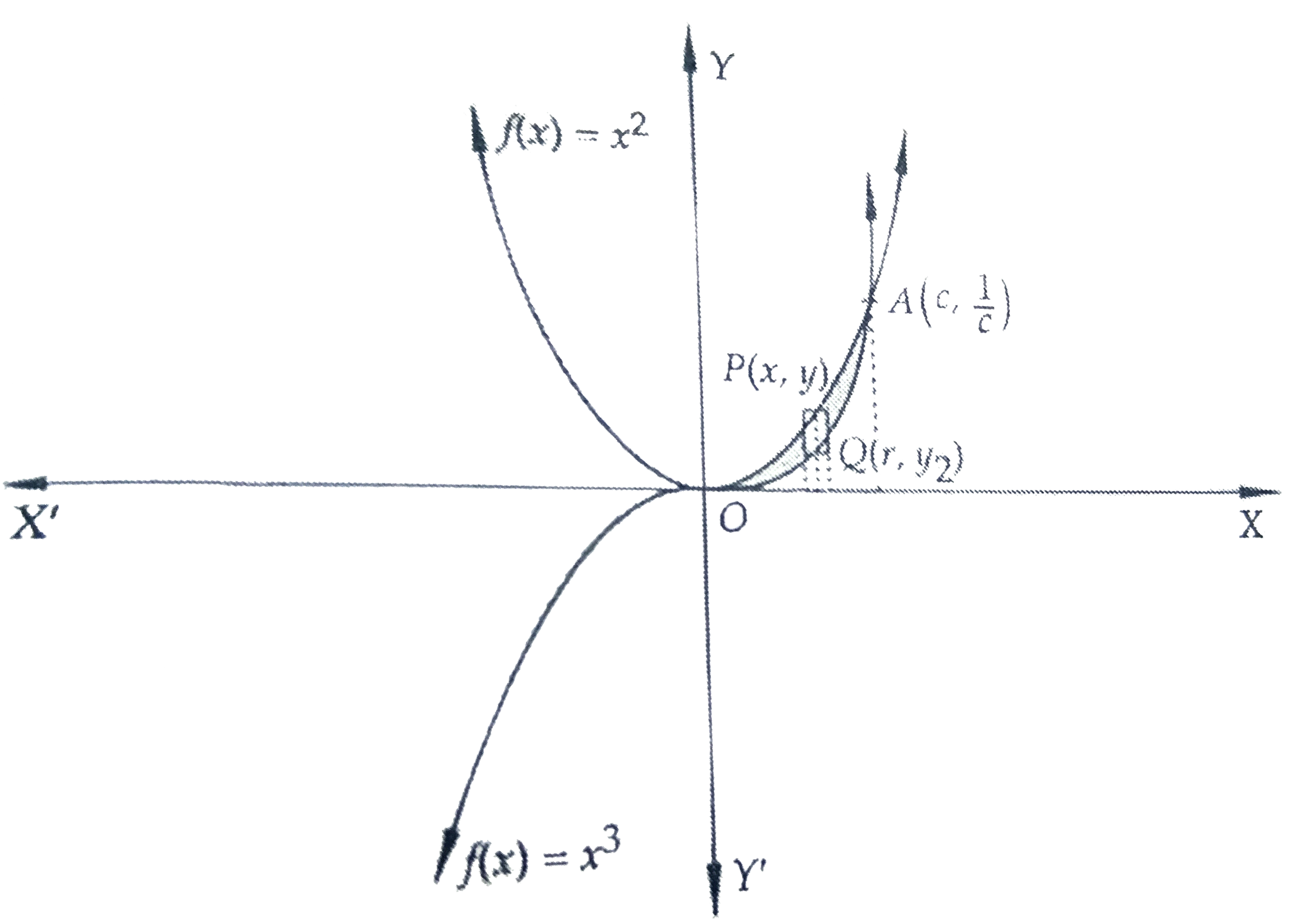
∴1/c∫0(y1−y2)dx=23
⇒1/c∫0(x2−cx3)dx=23
⇒[x33−cx44]1/c0=23
=112c3−23⇒c=12
Hence, 1c+1c2=2+4=6.
Topper's Solved these Questions
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise
61 Videos
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise
39 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
The value of c in Lgrange's Mean Value theorem for the function f(x) =x(x-2) in the interval [1,2] is
A32B23C34D54
If x lies in the interval [0, 1] , then the least value of x2+x+1 is (a) 3 (b) 3/4 (c) 1 (d) none of these
View SolutionThe fucntion f(x)=x3−6ax2+5x satisfies the conditions of Lagrange's mean value theorem over the interval [1,2] and the value of c (that of LMVT) is 74, then find the value of a.
View SolutionIf A > 0, c,d,u.v are non-zero constants and the graph of f(x)=|Ax+c|+d and g(x)=−|Ax+u|+v intersect exactly at two points (1,4) and (3,1), then the value of u+cA equals
View SolutionSuppose that the quadratic function f(x)=ax2+bx+c is non-negative on the interval [-1,1] . Then, the area under tha graph of f over the interval [-1,1] and the X - axis is given by the formula
View SolutionA function y=f(x) has a second-order derivative f''(x)=6(x−1). It its graph passes through the point (2,1) and at that point tangent to the graph is y=3x−5, then the value of f(0) is 1 (b) −1 (c) 2 (d) 0
View SolutionLet f(x) = Max. {x2,(1−x)2,2x(1−x)} where x∈[0,1] If Rolle's theorem is applicable for f(x) on largestpossible interval [a, b] then the value of 2(a+b+c) when c∈[a,b] such that f'(c) = 0, is
View SolutionIf the integral I=∫ex2x3dx=ex2f(x)+c, where c is the constant of integration and f(1)=0, then the value of f(2) is equal to
View Solution
