If A > 0, c,d,u.v are non-zero constants and the graph of f(x)=|Ax+c|+d and g(x)=−|Ax+u|+v intersect exactly at two points (1,4) and (3,1), then the value of u+cA equals
4
-4
2
-2
The correct Answer is:B
To solve the problem, we need to analyze the given functions and their intersection points. The functions are:
1. f(x)=|Ax+c|+d
2. g(x)=−|Ax+u|+v
We know that these functions intersect at the points (1, 4) and (3, 1). This means that at these points, the values of f(x) and g(x) are equal.
Step 1: Set up the equations based on the intersection points
At the point (1, 4):
f(1)=g(1)=4
So, we have:
|A(1)+c|+d=4(1)
−|A(1)+u|+v=4(2)
At the point (3, 1):
f(3)=g(3)=1
So, we have:
|A(3)+c|+d=1(3)
−|A(3)+u|+v=1(4)
Step 2: Analyze the equations
From equations (1) and (2):
1. |A+c|+d=4
2. −|A+u|+v=4
From equations (3) and (4):
3. |3A+c|+d=1
4. −|3A+u|+v=1
Step 3: Solve for d and v
From (1) and (3), we can express d:
d=4−|A+c|(from 1)
d=1−|3A+c|(from 3)
Setting these equal gives:
4−|A+c|=1−|3A+c|
|3A+c|−|A+c|=3(5)
From (2) and (4), we can express v:
v=4+|A+u|(from 2)
v=1+|3A+u|(from 4)
Setting these equal gives:
4+|A+u|=1+|3A+u|
|3A+u|−|A+u|=3(6)
Step 4: Solve equations (5) and (6)
Now we have two equations (5) and (6). We can analyze these equations to find relationships between u,c, and A.
From equation (5):
- The absolute value expressions imply two cases based on the values of A+c and 3A+c.
From equation (6):
- Similarly, we analyze the absolute values of A+u and 3A+u.
Step 5: Find u+cA
After solving the equations, we can find the value of u+c in terms of A.
From the analysis, we find:
u+cA=−4
Final Answer
Thus, the value of u+cA is:
−4
2. g(x)=−|Ax+u|+v
f(1)=g(1)=4
So, we have:
|A(1)+c|+d=4(1)
−|A(1)+u|+v=4(2)
f(3)=g(3)=1
So, we have:
|A(3)+c|+d=1(3)
−|A(3)+u|+v=1(4)
1. |A+c|+d=4
2. −|A+u|+v=4
3. |3A+c|+d=1
4. −|3A+u|+v=1
d=4−|A+c|(from 1)
d=1−|3A+c|(from 3)
4−|A+c|=1−|3A+c|
|3A+c|−|A+c|=3(5)
v=4+|A+u|(from 2)
v=1+|3A+u|(from 4)
4+|A+u|=1+|3A+u|
|3A+u|−|A+u|=3(6)
- The absolute value expressions imply two cases based on the values of A+c and 3A+c.
- Similarly, we analyze the absolute values of A+u and 3A+u.
u+cA=−4
−4
Topper's Solved these Questions
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise (More Than One Correct Option Type Questions)
22 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise (Statement I And Ii Type Questions)
11 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - Exercise For Session 12
4 Videos
- ESSENTIAL MATHEMATICAL TOOLS BOOK - ARIHANT MATHS ENGLISHCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)
3 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
Similar Questions
Knowledge Check
If f(x) =ax2+bx+c and f(1)=3 and f(-1)=3, then a+c equals
A-3B0C2D3
A straight line passes through the points A(-5, 2) and B(3,-6). It intersects the co-ordinate axes at points C and D . Find :
the equation of AB.
View SolutionConsider two curves C1:y2=4x ; C2=x2+y2−6x+1=0. Then, a. C1 and C2 touch each other at one point b. C1 and C2 touch each other exactly at two point c. C1 and C2 intersect(but do not touch) at exactly two point d. C1 and C2 neither intersect nor touch each other
View SolutionSuppose a parabola y=x2−ax−1 intersects the coordinate axes at three points A,B and C, respectively. The circumcircle of ΔABC intersects the y-axis again at the point D(0,t). Then the value of t is
View SolutionIf set of values a for which f(x)=ax2−(3+2a)x+6,a≠0 is positive for exactly three distinct negative integral values of x is (c,d] , then the value of (c2+4|d|) is equal to ________.
View SolutionIf fandg are the function whose graphs are as shown, let u(x)=f(g(x)),w(x)=g(g(x))
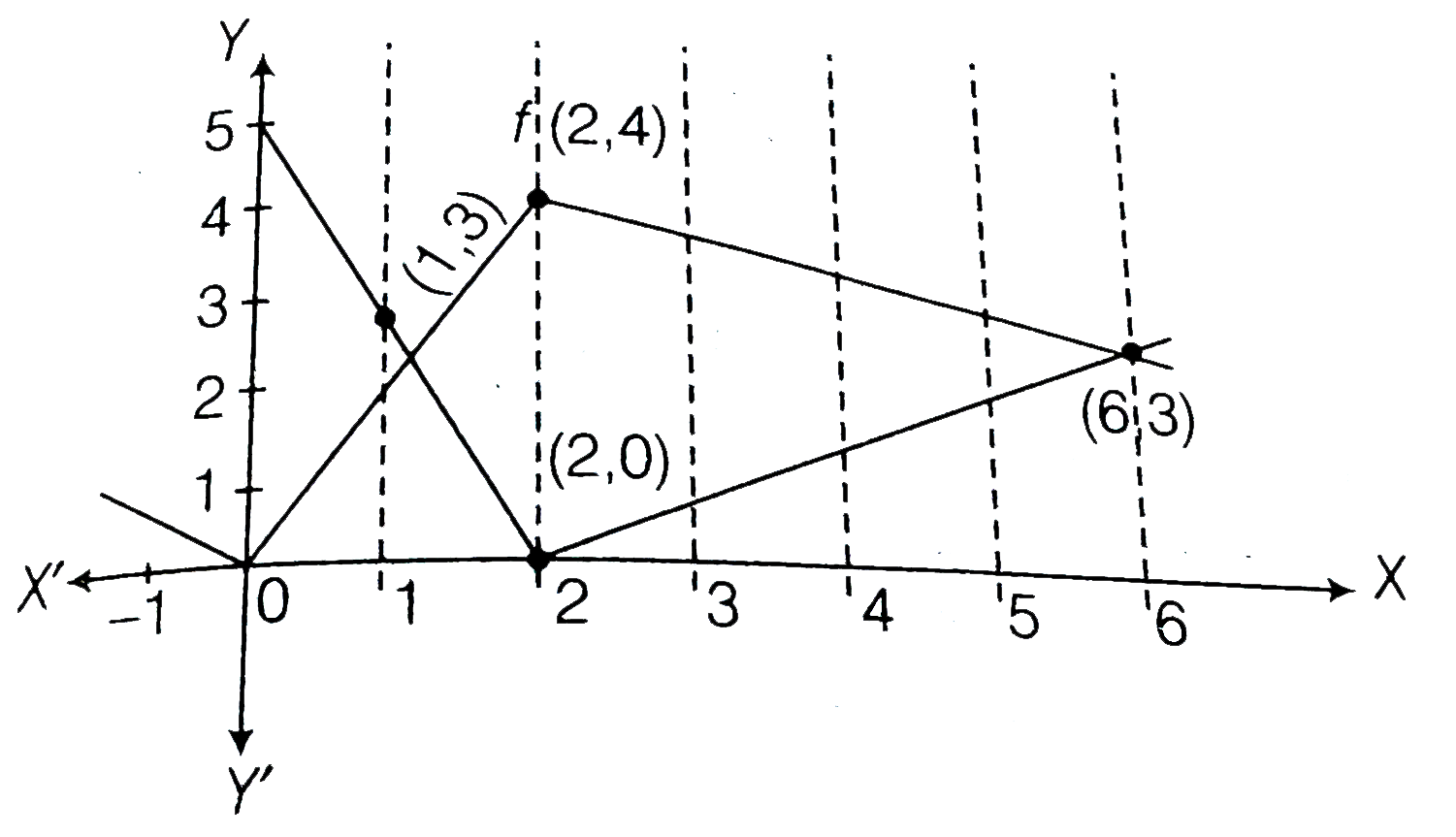 Then the value of u'(1)+w'(1) is
Then the value of u'(1)+w'(1) is
View SolutionIf f(x)=log{u(x)v(x)}, u(1)=v(1) and u′(1)=v′(1)=2 , then find the value of f′(1) .
View SolutionIf f(x)=log{u(x)v(x)}, u(1)=v(1) and u′(1)=v′(1)=2 , then find the value of f′(1) .
View Solution
