If one the roots fo the equation is the cube of the othere for all , then f(x)=
none of these
The correct Answer is:B
Let and be the roots of the equation . Then,
, where
Topper's Solved these Questions
- REAL FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:REAL FUNCTIONS Exercise:Section II - Assertion Reason Type
Explore 8 Videos
- REAL FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:REAL FUNCTIONS Exercise:Exercise
Explore 94 Videos
- REAL FUNCTIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:REAL FUNCTIONS Exercise:Chapter Test
Explore 58 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBook:OBJECTIVE RD SHARMA ENGLISHChapter:PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMExercise:Chapter Test
Explore 55 Videos
- SCALAR AND VECTOR PRODUCTS OF THREE VECTORS Book:OBJECTIVE RD SHARMA ENGLISHChapter:SCALAR AND VECTOR PRODUCTS OF THREE VECTORS Exercise:Exercise
Explore 63 Videos
Similar Questions
Knowledge Check
If f(x)≥0 for all x, then f(2-x) is
A≥−2B≥0C≥2D≤0
Consider the graph of y = f(x) as shown in the following figure.
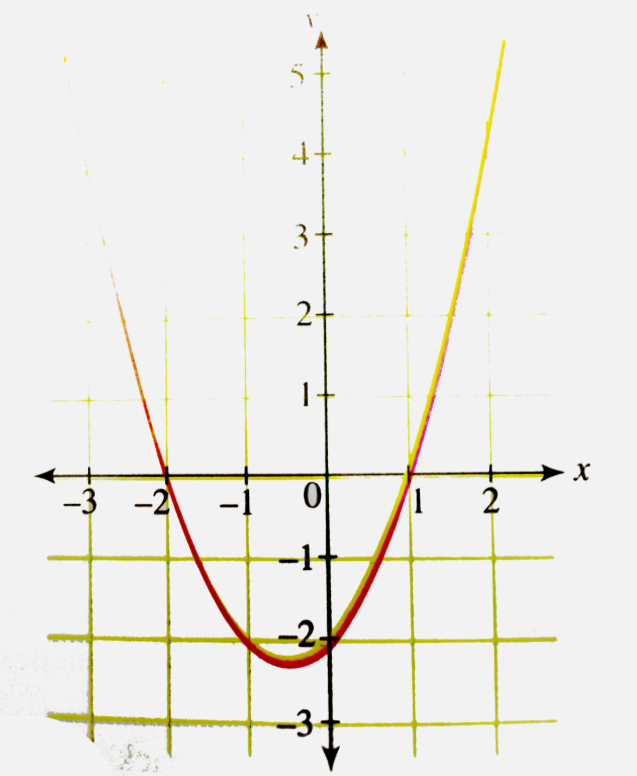
(i) Find the sum of the roots of the equation f (x) = 0.
(ii) Find the product of the roots of the equation f(x) = 4.
(iii) Find the absolute value of the difference of the roots of the equation f(x) = x+2 .
View SolutionFind the number of real roots of the equation f(x)=x3+2x2+x+2=0
View SolutionIf a real valued function f(x) satisfies the equation f(x+y)=f(x)+f(y) for all x,y∈R then f(x) is
View SolutionStatement -1 : one root of the equation x2+5x−7=0 lie in the interval (1,2).
and
Statement -2 : For a polynomial f(x),if f(p)f(q) lt 0, then there exists at least one real root of f(x) =0 in (p,q)
View SolutionStatement-1: Ifαandβ are real roots of the quadratic equations ax2+bx+c=0and−ax2+bx+c=0, then a2x2+bx+c=0 has a real root between αandβ
Statement-2: If f(x) is a real polynomial and x1,x2∈R such that f(x1)fx2<0, then f(x) = 0 has at leat one real root between x1andx2.
View SolutionA function f:R→R satisfies the equation f(x+y)=f(x)f(y) for allx,y∈R and f(x)≠0 for all x∈R. If f(x) is differentiable at x=0andf′(0)=2, then prove that f′(x)=2f(x).
View SolutionIf f(x)>x;∀x∈R. Then the equation f(f(x))−x=0, has
View Solution