The greph of y=x3+ax2+bx+c has no extemun if and only if
a2=b
a2<3b
a2>2b
a2>2b2
The correct Answer is:B
We have
y=x3+ax2+bx+c⇒dydx=3x2+2ax+b
Clearly dydx>0if4a2−12b<0
⇒y=f(x) has no extremum iff a2<3b
Hence, f(x) has no extremum iff a2<3b
Topper's Solved these Questions
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Section II - Assertion Reason Type
7 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Exercise
47 Videos
- MAXIMA AND MINIMA BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MAXIMA AND MINIMA EXERCISE - Chapter Test
29 Videos
- MATHEMATICAL REASONING BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - Chapter Test
20 Videos
- MEASURES OF CENTRAL TENDENCYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - Chapter Test
21 Videos
Similar Questions
The adjoining graph of y=ax2+bx+c shows that
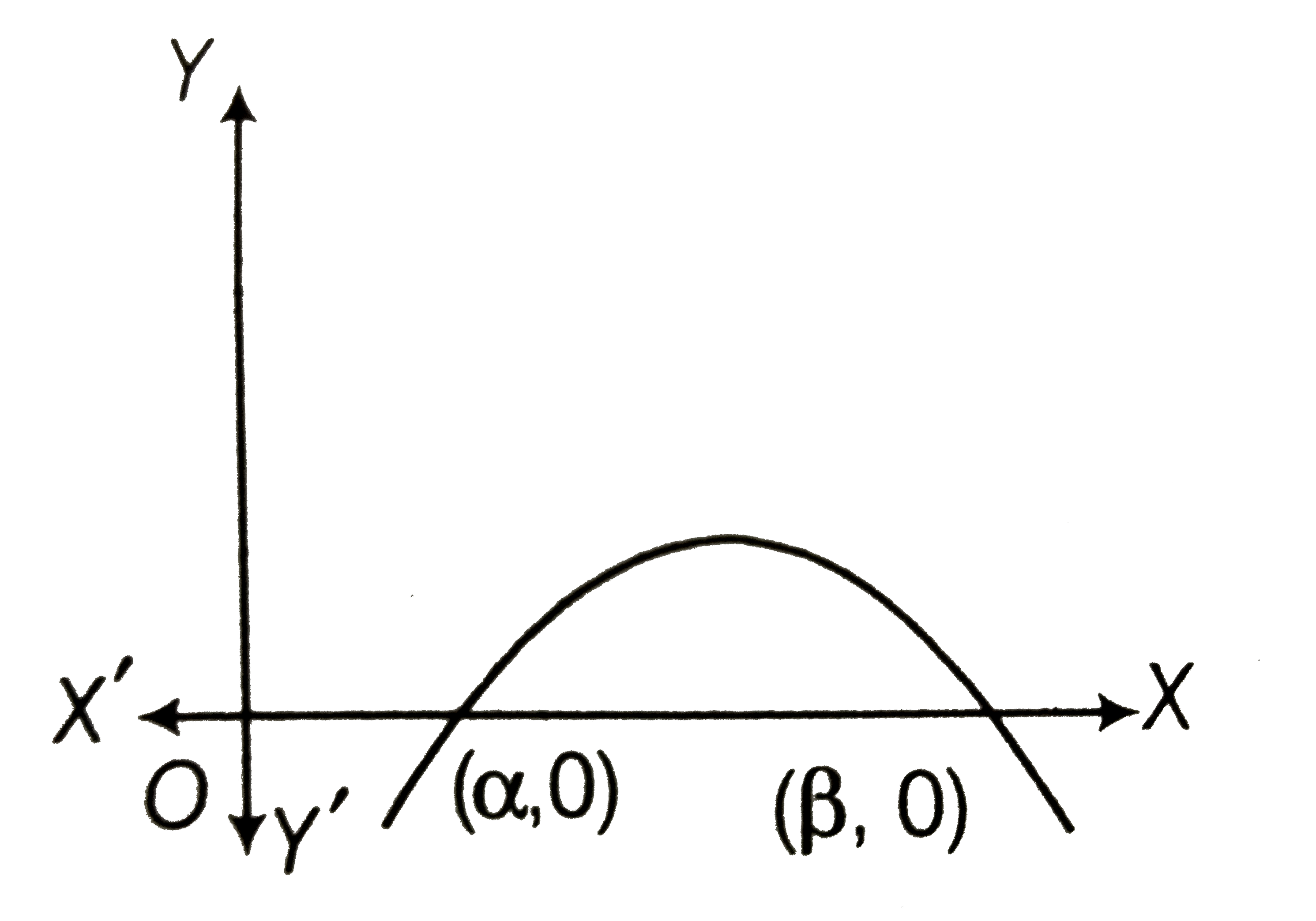
View SolutionIf the graph of y=ax2+bx+c lies completely above the x-axis, then
View SolutionIf f(x) =X3+ax2+bx+c has extreme values at x=-1 and x=3 . Find a,b,c.
View SolutionIf the equation x3−3ax2+3bx−c=0 has positive and distinct roots, then
View Solutionax2+2bx−3c=0 has no real root and a+b>3c4 then
View SolutionIf 4a+2b+c=0 , then the equation 3ax2+2bx+c=0 has at least one real lying in the interval
View SolutionIf two roots of x3−ax2+bx−c=0 are equal in magnitude but opposite in sign. Then:
View SolutionSuppose 1,2,3 are the roots of the equation x4+ax2+bx+c=0. Find the value of c.
View SolutionThe vertex or the parabola y = ax2+bx+c is
View SolutionIf the curve y=ax2+bx+c passes through the point (1, 2) and the line y = x touches it at the origin, then
View Solution
