Question

Let A,B and C be three sets of complex numbers as defined below: ${\displaystyle \begin{array}{ll}& A=\{z:Im\left(z\right)\ge 1\}\\ & B=\{z:\left|z-2-i\right|=3\}\\ & C=\{z:Re(1-i)z)=3\sqrt{2}\text{where}i=\sqrt{-1}\end{array}}$
The number of elements in the set ${\displaystyle A\cap B\cap C}$, is

Options

A. 0
B. 1
C. 2
D. `infty`

Answer

B

Explanation

Let `z=x+iy`. Then,
`(1-i)z=(1-i)(x+iy)=(x+iy)+i(y-x)`
`rArr "Re"{(1-i)z}=x+y`
`therefore {(1-i)z}=sqrt(2) rArr x+y=sqrt(2)`

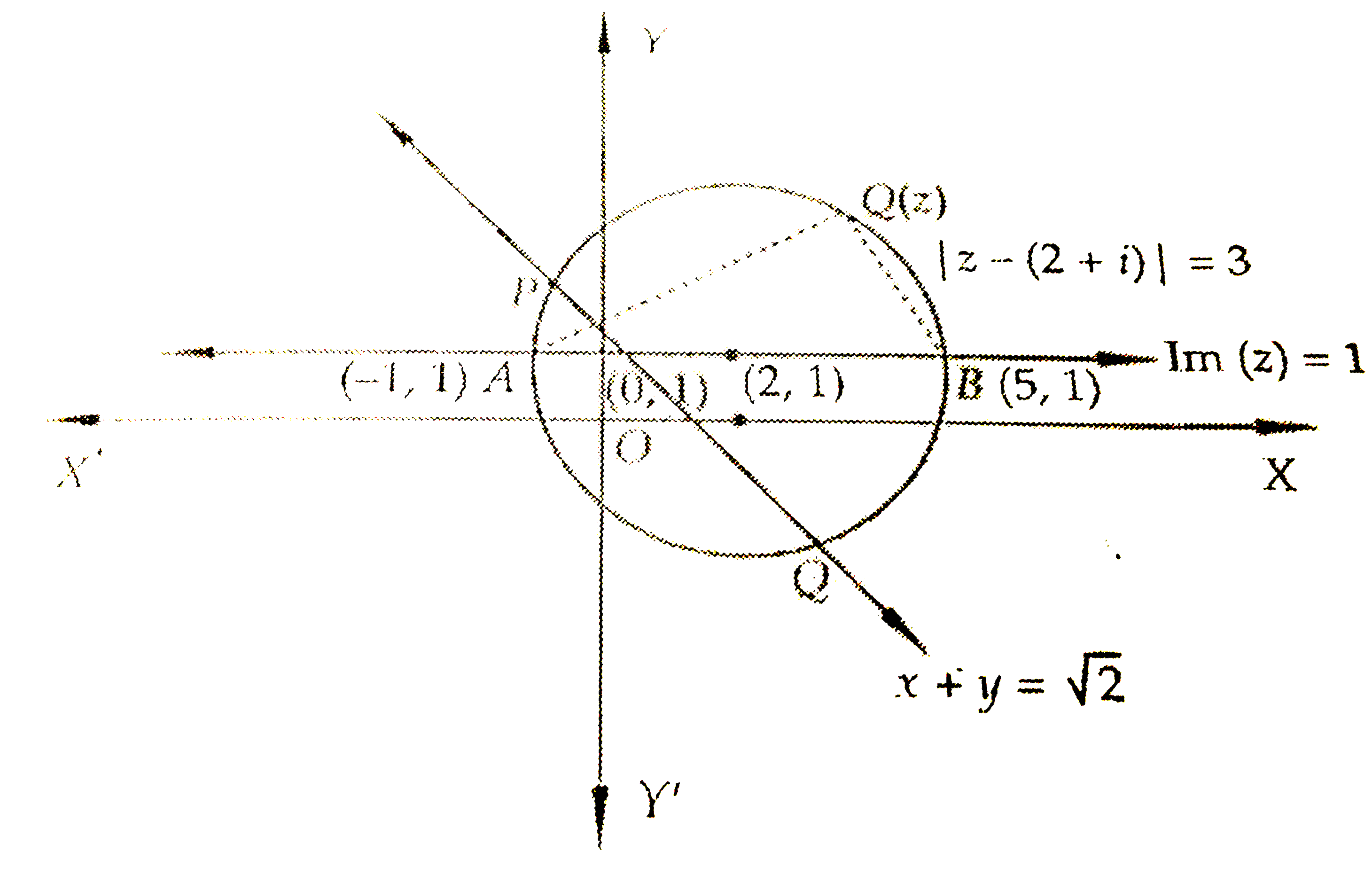
Clearly, A is the set of all points lying on or above the line y=1 in xy-plane, B is the set of all points lying on the circle having center at (2,1) and radius 3 and C is the set of all points on the line `x+y=sqrt(2)`.
The line `x+y=sqrt(2)` intersects the circle `|z-(2+i)|=3` at P and Q out of which P lies in the region represented by Im `(z) ge 1`.
`therefore A frown B frown C` contains exactly one point.