Let z1 and z2 be two distinct complex numbers and z=(1−t)z1+tz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
|z−z2|+|z−z2|=|z1−z2|
arg(z−z1)=arg(z−z2)
∣∣∣z−z1¯z−¯z1z2−z1¯z2−¯z1∣∣∣=0
arg(z−z1)=arg(z2−z1)
The correct Answer is:B
Let z1 and z2 be represented by points A and B respectively in the Argand plane.
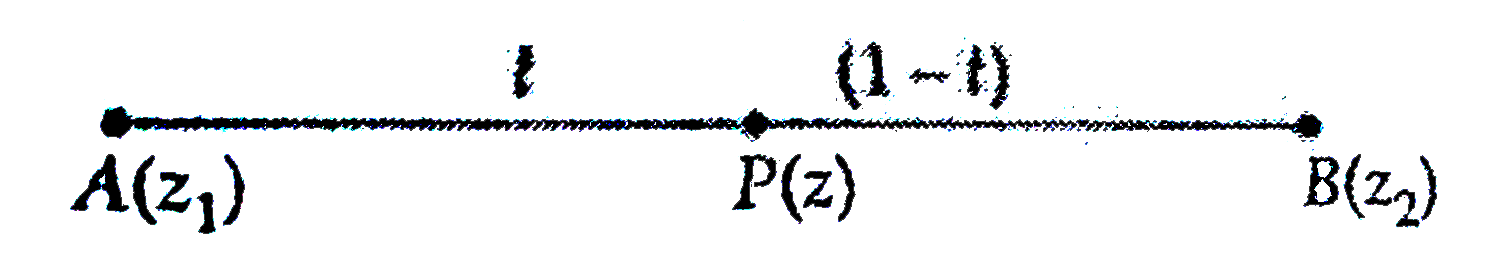
We have,
z=(1−t)z1+tz2(1−t)+t
⇒ z represents a point P dividing AB in the ratio t:(1−t)
Clearly, AP+PB=AB
⇒|z−z1|+|z−z2|=|z1−z2|
So, option (a) is true.
Since, A,P,B are collinear. Therefore,
arg(¯¯¯AP)=arg(¯¯¯AB)⇒arg(z−z1)=arg(z2−z1)
So, option (d) is correct.
We have,
z=(1−t)z1+tz2
⇒t=z−z1z2−z1 is purely real
⇒|(z−z1,¯z−¯z1),(z2−z1,¯z2,¯z1)|=0
Hence, option (c) is correct.
We have,
arg(z−z1)=arg(¯¯¯AP) and arg(z−z−(2))=arg(¯¯¯BP)
Clearly, arg(¯¯¯AP)−arg(z−z2)≠0
So, option (b) is not correct.
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Exercise
129 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test
53 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
87 Videos
Similar Questions
Let z1,z2 be two complex numbers such that z1+z2 and z1z2 both are real, then
View SolutionIf z1 and z2 are two complex numbers such that ∣∣∣z1−z2z1+z2∣∣∣=1, then
View SolutionLet z1,z2 be two complex numbers such that |z1+z2|=|z1|+|z2|. Then,
View SolutionIf z and w are two non-zero complex
numbers such that z=-w.
View SolutionIf z1andz2 are two complex numbers such that |z1|=|z2|, then is it necessary that z1=z2
View SolutionIf a complex number z satisfies |2z+10+10i|≤5√3−5, then the least principal argument of z is
View SolutionLet z1andz2 be two given complex numbers such that z1z2+z2z1=1and|z1|=3, then |z1−z2|2 is equal to
View SolutionLet z1andz2 be two distinct complex numbers and let z=(1−t)z1+tz2 for some real number t with 0<t<1. If a r g(w) denotes the principal argument of a nonzero complex number w , then
|z−z1|+|z−z2|=|z1−z2| (z−z1)=(z−z2)
∣∣z−z1z−(z)1z2−z1(z)2−(z)1∣∣=0
arg(z−z1)=arg(z2−z1)
View SolutionFill in the blanks.
If z1 and z2 are complex numbers such that z1+z2 is a real number, then z1=….
View SolutionLet z1,z2 be two complex numbers with |z1|=|z2|. Prove that (z1+z2)2z1z2 is real.
View Solution
