Let S=S1∩S2∩S3, where s1={z∈C|z∣<4},S2={z∈C:ln[z−1+√3i1−√31]>0}and
S3={z∈C:Rez>0} Area of S=
10π3
20π3
16π3
32π3
The correct Answer is:B
Clearly, S1 represents the interior of the region bounded by the circle having center at the origin and radius 4 units.

Let z=x+iy, then
z−1+i√31−i√3=x+iy1−i√3−1
=⎛⎜
⎜⎝(x+iy)1+i√3(1−i√3)(1+i√3)−1⎞⎟
⎟⎠=x−√3y−44+iy+√3x4
∴Imz−1+i√31−i√30>0⇒(y+√3x4)>0⇒y>−√3x
Thus, S2 represents the region lying above the line y=−√3x. Clearly, S3 represents region representing on the right sides of y-axis.
Hence, S=S1⌢S2⌢S3 represents the shaded region shown in Fig.
Area of region S =Area of semi cricel -Area of the sector OB′C
=12π(4)2−12(4)2×π6=20π3 sq. units.
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Exercise
129 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Chapter Test
53 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
87 Videos
Similar Questions
Let S=S1∩S2∩S3, where s1={z∈C|z∣<4},S2={z∈C:ln[z−1+√3i1−√31]>0}and
S3={z∈C:Rez>0} Area of S=
View SolutionLet S=S1∩S2∩S3, where S1={zinC:|z|<4},
S2={z inC:Im[z−1+√3i1−√3i]>0}andS3={zinC:Rez>0}
minz∈S|1−3i−z|=
View SolutionLet w = (√3+ι2) and P={wn:n=1,2,3,.....}, Further H1={z∈C:Re(z)>12}andH2={z∈c:Re(z)<−12} Where C is set of all complex numbers. If z1∈P∩H1,z2∈P∩H2 and O represent the origin, then ∠Z1OZ2 =
View SolutionLet 0≠a,0≠b∈R. Suppose
S={z∈C,z=1a+ibtt∈R,t≠0}, where i=√−1. If z=x+iy and z∈S, then (x,y) lies on
View SolutionThe equation of a circle S1 is x2+y2=1. The orthogonal tangents to S1 meet at another circle S2 and the orthogonal tangents to S2 meet at the third circle S3. Then (A) radius of S2andS3 are in ratio 1:√2 (B) radius of S2andS1 are in ratio 1:2 (C) the circles S1,S2andS3 are concentric (D) none of these
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. The co-ordinates of P1 are :
View SolutionLet each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
The ratio area(ΔP1P2P3)area(ΔC1C2C3) is equal to
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. P2andP3 are image of each other with respect to line :
View SolutionConsider the region S of complex numbers a such that ∣∣z2−az+1∣∣=1, where |z|=1 . Then area of S in the Argand plane is
View SolutionIn the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
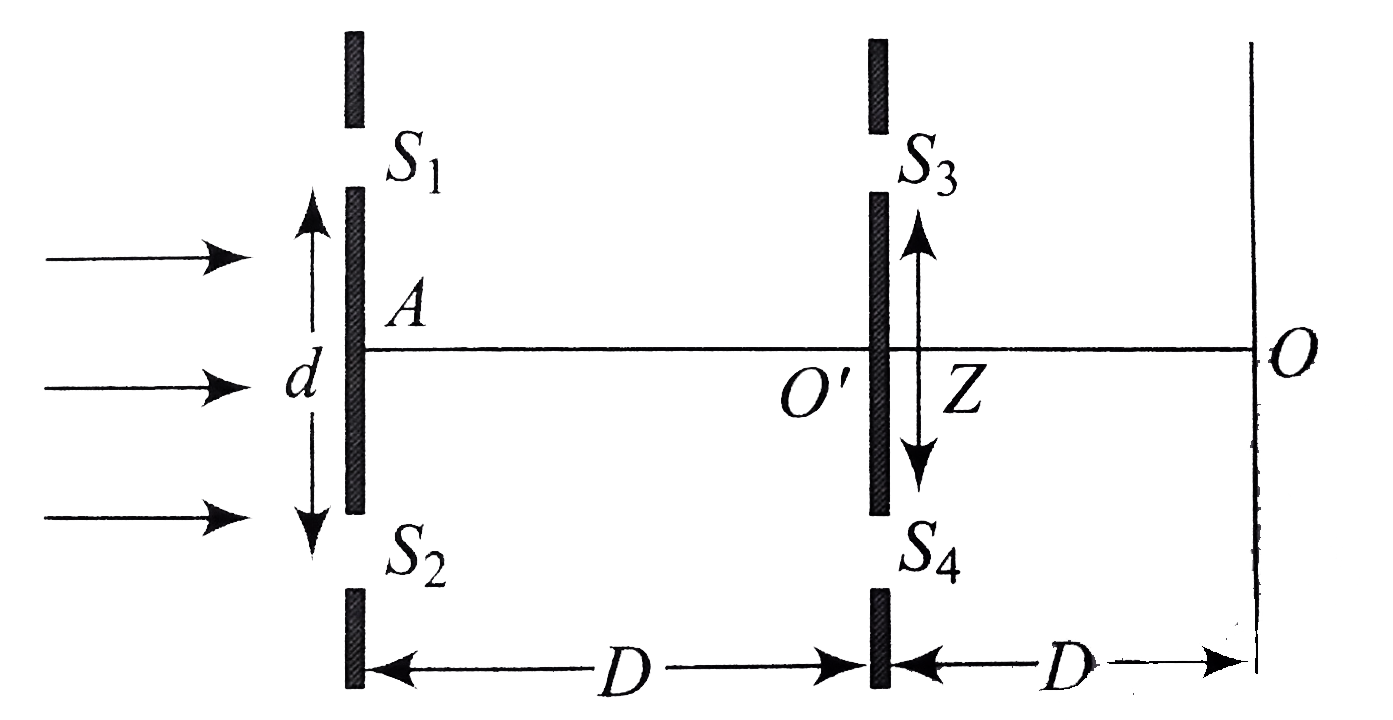
The minimum value of Z for which the intensity at O is zero is
View Solution
