IfA={x,y):x2+y2=25}and
B={(x,y):x2+9y2=144}, then A∩B contains
one point
three point
two point
four point
The correct Answer is:four point
To find the intersection of the sets A and B, we need to analyze the equations given for each set.
1. Identify the equations of the sets:
- Set A: x2+y2=25
- Set B: x2+9y2=144
2. Understand the shapes represented by the equations:
- The equation x2+y2=25 represents a circle centered at the origin (0, 0) with a radius of 5.
- The equation x2+9y2=144 represents an ellipse centered at the origin. To put it in standard form, we can divide the entire equation by 144:
x2144+y216=1
This indicates that the semi-major axis (along the x-axis) is 12 and the semi-minor axis (along the y-axis) is 4.
3. Graph the equations:
- Draw the circle with radius 5 and the ellipse with semi-major axis 12 and semi-minor axis 4. The circle will be completely inside the ellipse since its radius is smaller than the semi-major axis of the ellipse.
4. Find the points of intersection:
- To find the points where the circle and the ellipse intersect, we can substitute y2 from the circle's equation into the ellipse's equation.
- From the circle's equation, we have:
y2=25−x2
- Substitute y2 into the ellipse's equation:
x2+9(25−x2)=144
Simplifying this gives:
x2+225−9x2=144
−8x2+225=144
−8x2=144−225
−8x2=−81
x2=818
x=±√818=±9√8=±9√24
5. Find corresponding y values:
- Substitute x2=818 back into the circle's equation to find y2:
y2=25−818=2008−818=1198
y=±√1198=±√1192√2=±√2384
6. Count the points of intersection:
- Since x can take on two values (+9√24 and −9√24) and y can also take on two values (+√2384 and −√2384), we can find a total of 2×2=4 points of intersection.
Thus, the intersection A∩B contains 4 points.
- Set A: x2+y2=25
- Set B: x2+9y2=144
- The equation x2+y2=25 represents a circle centered at the origin (0, 0) with a radius of 5.
- The equation x2+9y2=144 represents an ellipse centered at the origin. To put it in standard form, we can divide the entire equation by 144:
x2144+y216=1
This indicates that the semi-major axis (along the x-axis) is 12 and the semi-minor axis (along the y-axis) is 4.
- Draw the circle with radius 5 and the ellipse with semi-major axis 12 and semi-minor axis 4. The circle will be completely inside the ellipse since its radius is smaller than the semi-major axis of the ellipse.
- To find the points where the circle and the ellipse intersect, we can substitute y2 from the circle's equation into the ellipse's equation.
- From the circle's equation, we have:
y2=25−x2
- Substitute y2 into the ellipse's equation:
x2+9(25−x2)=144
Simplifying this gives:
x2+225−9x2=144
−8x2+225=144
−8x2=144−225
−8x2=−81
x2=818
x=±√818=±9√8=±9√24
- Substitute x2=818 back into the circle's equation to find y2:
y2=25−818=2008−818=1198
y=±√1198=±√1192√2=±√2384
- Since x can take on two values (+9√24 and −9√24) and y can also take on two values (+√2384 and −√2384), we can find a total of 2×2=4 points of intersection.
Topper's Solved these Questions
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Exercise
45 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test
59 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Chapter Test
34 Videos
Similar Questions
Knowledge Check
In the hyperbola16x2−9y2=144, the value of eccentricity is
A13B43C53D73
In some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
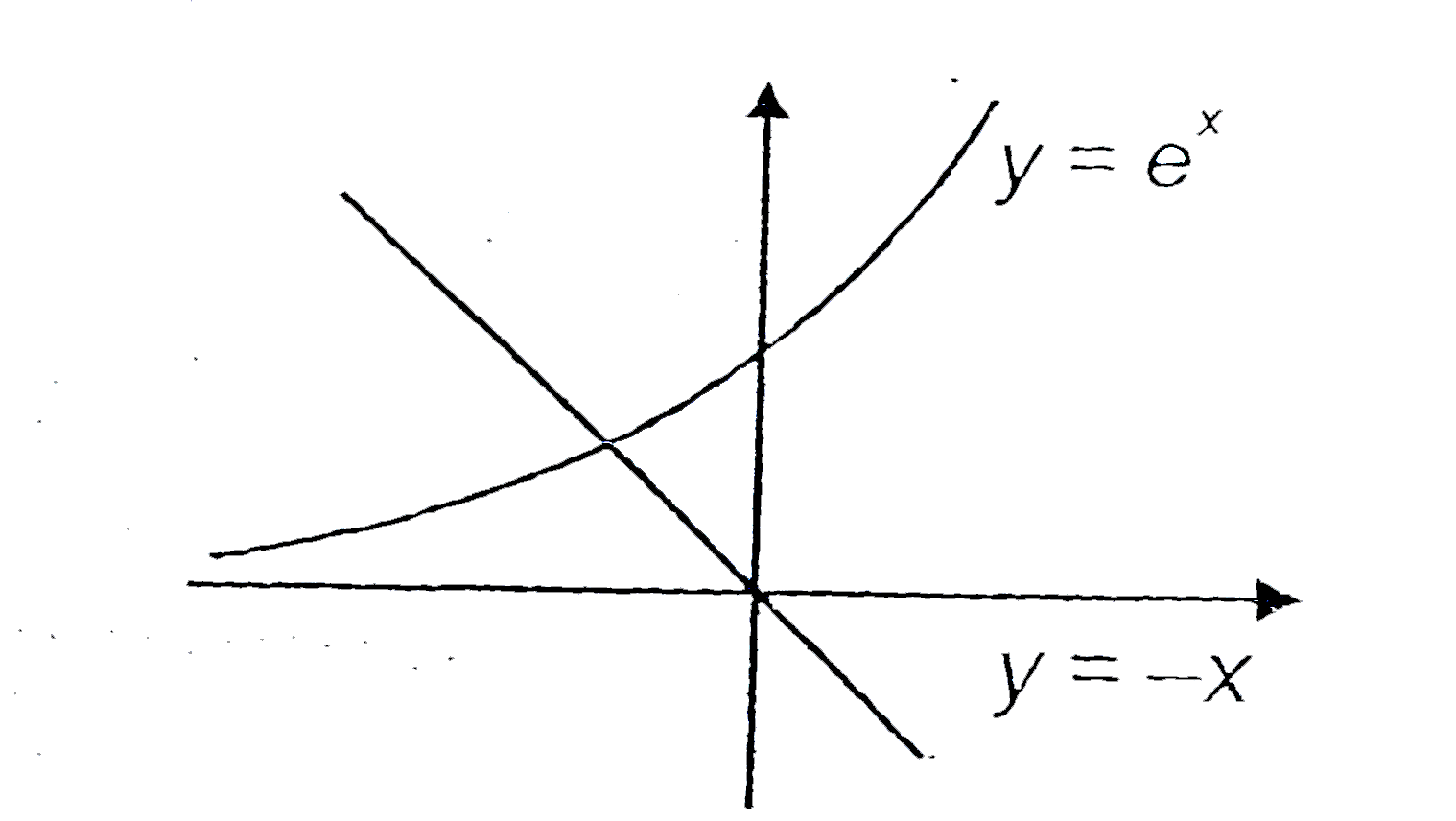
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
View SolutionifA={(x,y):x2+y2≤1,x,y∈R]and
B={(x,y):x2+y2≤x2+y2≤4,x,y∈R]then
View SolutionIf a=xx2+y2andb=yx2+y2. The value of (x+y) is
View SolutionIf the regions A and B are given by A={(x,y)/:y>x}B={(x,y):y<2−x2} then the area of A∩B is
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
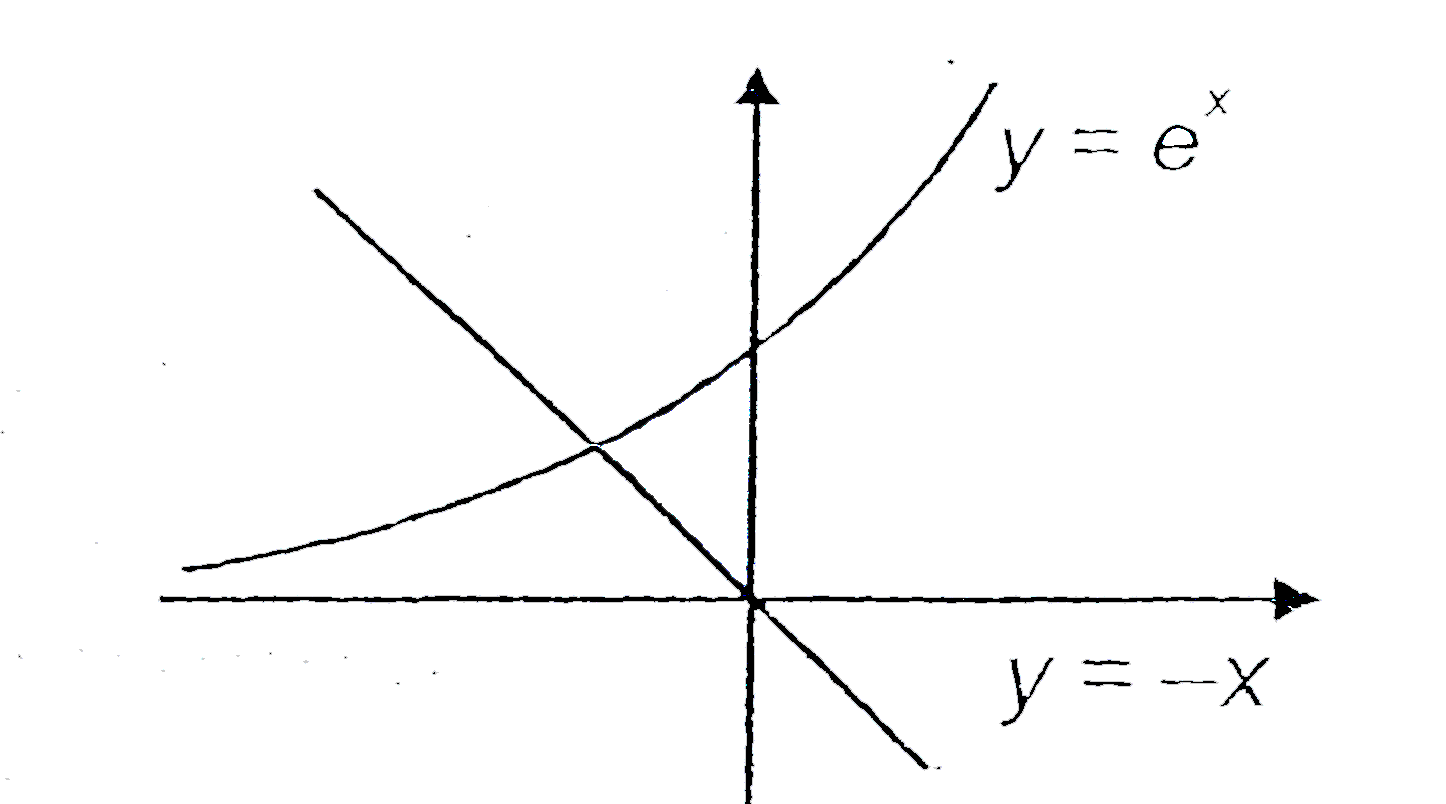
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View SolutionA point chanrge of magnitude q=4.5nC is moving with speed v=3.6×107ms−1 parallel to the x-axis along the line y=3m. Find the magnetic field at the origin produced by this charge when the charge is at the point x=−4m, y=3m, as shown in Fig.

View SolutionThe diameter of 16x2−9y2=144 which is conjugate to x=2y is
View Solution
