If the regions A and B are given by then the area of is
a)
b)
c)
d)
The correct Answer is:B
To find the area of the intersection of the regions A and B given by:
- A={(x,y):y>x}
- B={(x,y):y<2−x2}
we need to follow these steps:
Step 1: Find the intersection points of the curves
We have the line y=x and the parabola y=2−x2. To find the intersection points, we set these two equations equal to each other:
x=2−x2
Rearranging gives:
x2+x−2=0
Step 2: Solve the quadratic equation
We can factor the quadratic equation:
(x+2)(x−1)=0
Thus, the solutions are:
x=−2andx=1
Step 3: Find corresponding y-values
Using y=x:
- For x=−2, y=−2 (point: (−2,−2))
- For x=1, y=1 (point: (1,1))
Step 4: Set up the integral for the area
The area of the intersection A∩B can be found by integrating the difference between the upper curve (the parabola) and the lower curve (the line) from x=−2 to x=1:
Area=∫1−2((2−x2)−x)dx
Step 5: Simplify the integrand
Simplifying the integrand gives:
2−x2−x=2−x−x2
Step 6: Integrate
Now we integrate:
∫1−2(2−x−x2)dx
This can be split into three separate integrals:
∫1−22dx−∫1−2xdx−∫1−2x2dx
Calculating each integral:
1. ∫1−22dx=2(x)1−2=2(1−(−2))=2⋅3=6
2. ∫1−2xdx=(x22)1−2=122−(−2)22=12−2=−32
3. ∫1−2x2dx=(x33)1−2=133−(−2)33=13+83=3
Step 7: Combine the results
Now substituting back into the area calculation:
Area=6−(−32)−3=6+32−3=3+32=62+32=92
Final Answer
The area of the intersection A∩B is:
92 square units
- B={(x,y):y<2−x2}
- For x=1, y=1 (point: (1,1))
2. ∫1−2xdx=(x22)1−2=122−(−2)22=12−2=−32
3. ∫1−2x2dx=(x33)1−2=133−(−2)33=13+83=3
Similar Questions
The area of the region described by A={(x,y):x2+y2≤1andy2≤1−x} is
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
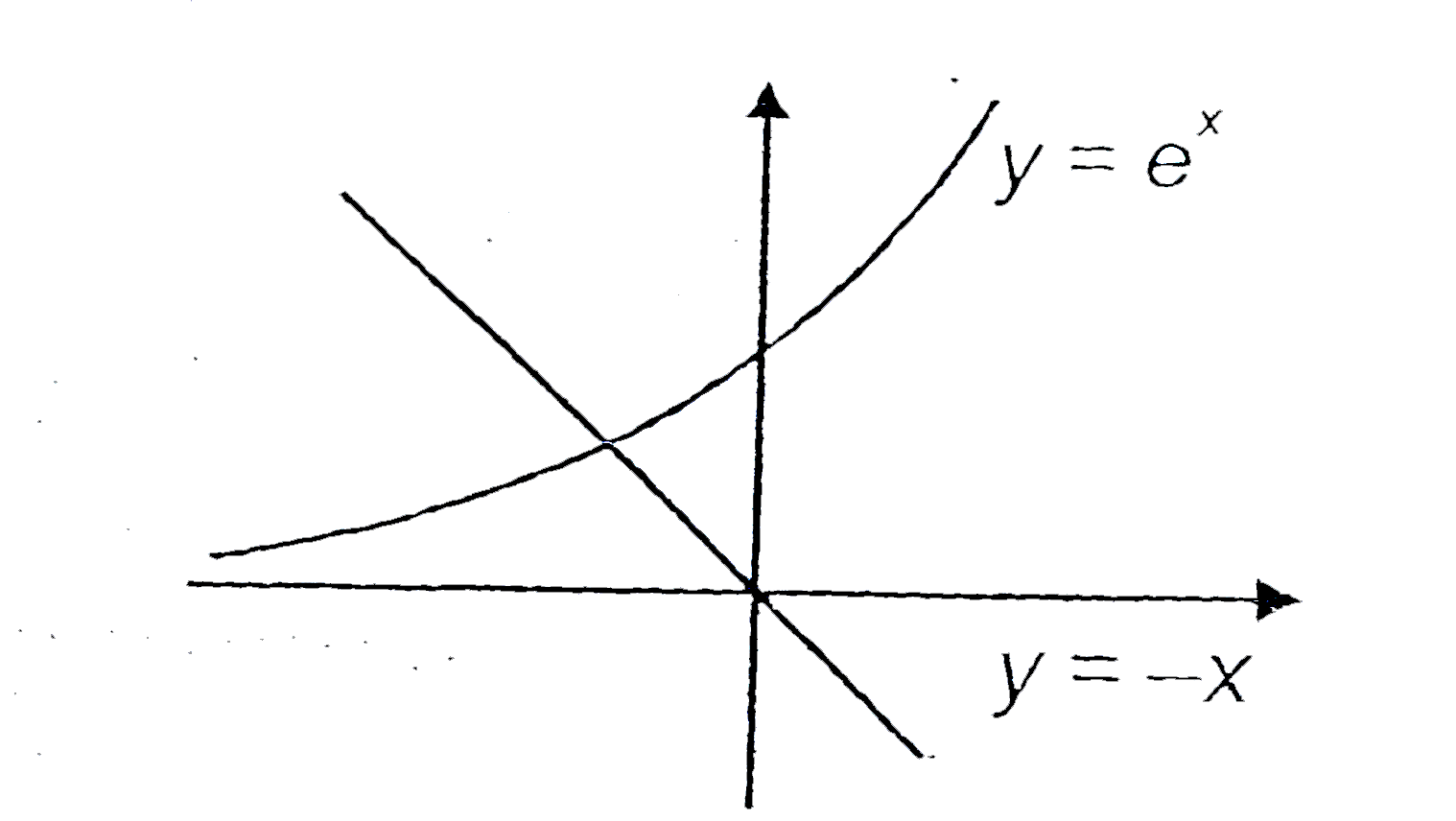
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
View SolutionConsider the regions A={(x,y)∣x2+y2≤100}andB=|xy|sin(x+y)>0} in the plane. Then the area of the region A∩B is
View SolutionIfA={x,y):x2+y2=25}and
B={(x,y):x2+9y2=144}, then A∩B contains
View SolutionArea of the region bounded by the curve y={x2x<0xx≥0 and the line y=4 is (A) 103 (B) 203 (C) 503 (D) none of these
View SolutionIf the area (in sq. units) of the region
{(x,y):y2≤4x,x+y≤1,x≥0,y≥0} is a√2+b, then a−b is equal to :
View SolutionThe area (in sq units) of the region {(x,y):y2≥2xandx2+y2≤4x,x≥0,y≥0} is
View SolutionArea of the region bounded by the curve {(x,y):x2a2+y2b2≤1≤xa+yb} is
View SolutionThe area of the region bounded by the curves {(x,y):x2+y2≤4,2≤x+y} is __________ .
View SolutionFind the area of the region {(x,y):x2+y2≤1≤x+y}.
View Solution
