ifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):x2+y2=9,x,y∈R},then
A−B=ϕ
B−A=B
A∩B≠ϕ
A∩B=A
The correct Answer is:B
To solve the problem, we need to analyze the sets A and B defined by the equations of circles.
Step 1: Define the sets A and B
The set A is defined as:
A={(x,y):x2+y2=4,x,y∈R}
This represents a circle with a radius of 2 centered at the origin (0,0).
The set B is defined as:
B={(x,y):x2+y2=9,x,y∈R}
This represents a circle with a radius of 3 centered at the origin (0,0).
Step 2: Analyze the intersection of sets A and B
To find the intersection A∩B, we need to check if there are any points that satisfy both equations:
1. x2+y2=4 (for set A)
2. x2+y2=9 (for set B)
Since no point can satisfy both equations simultaneously (as 4 is not equal to 9), we conclude that:
A∩B=∅
This means that there are no common elements between sets A and B.
Step 3: Calculate A - B
The difference A−B is defined as:
A−B=A∖(A∩B)
Since A∩B=∅, we have:
A−B=A
Thus, the elements of set A remain unchanged.
Step 4: Calculate B - A
Similarly, the difference B−A is defined as:
B−A=B∖(A∩B)
Again, since A∩B=∅, we have:
B−A=B
Thus, the elements of set B remain unchanged.
Conclusion
From the analysis above, we can summarize:
- A∩B=∅ (no intersection)
- A−B=A
- B−A=B
A={(x,y):x2+y2=4,x,y∈R}
This represents a circle with a radius of 2 centered at the origin (0,0).
B={(x,y):x2+y2=9,x,y∈R}
This represents a circle with a radius of 3 centered at the origin (0,0).
1. x2+y2=4 (for set A)
2. x2+y2=9 (for set B)
A∩B=∅
This means that there are no common elements between sets A and B.
A−B=A∖(A∩B)
Since A∩B=∅, we have:
A−B=A
Thus, the elements of set A remain unchanged.
B−A=B∖(A∩B)
Again, since A∩B=∅, we have:
B−A=B
Thus, the elements of set B remain unchanged.
- A∩B=∅ (no intersection)
- A−B=A
- B−A=B
Topper's Solved these Questions
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Section I - Solved Mcqs
24 Videos
- SEQUENCES AND SERIESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Chapter Test
59 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Chapter Test
34 Videos
Similar Questions
ifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):Y=|x|,x,y∈R} then
View SolutionifA={(x,y):x2+y2≤1,x,y∈R]and
B={(x,y):x2+y2≤x2+y2≤4,x,y∈R]then
View SolutionifA={(x,y):y=4x,x≠0}and
B={(x,y):x2+y2=8,x,y∈R},then
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
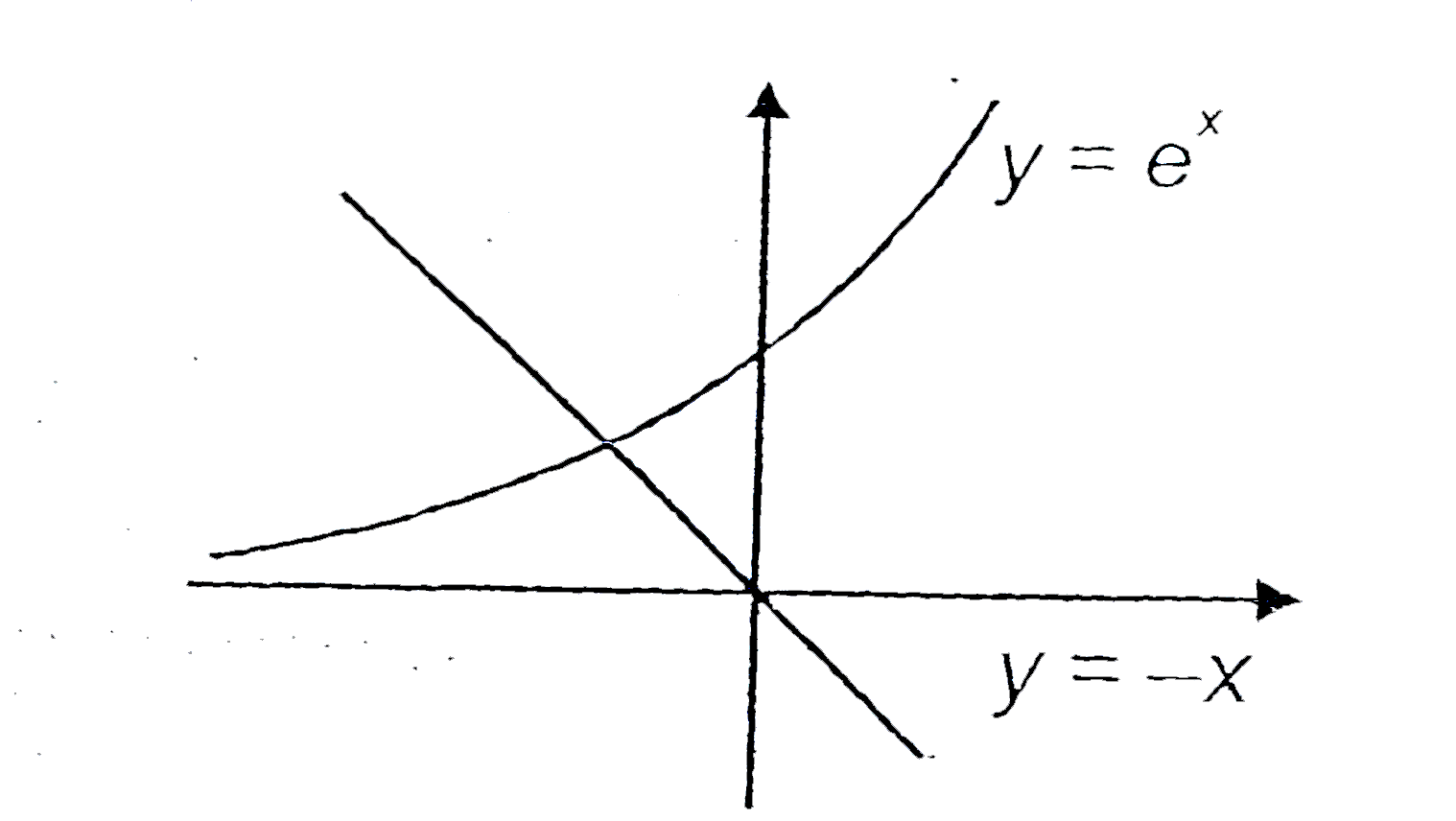
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
View SolutionIfA={x,y):x2+y2=25}and
B={(x,y):x2+9y2=144}, then A∩B contains
View SolutionWhich of the following are function: {(x,y):y2=x,x,y∈R} b. {(x,y):y=|x|,x,y∈R} c. {(x,y):x2+y2=1,x,y∈R} d. {(x,y):x2−y2=1,x,y∈R}
View SolutionIf A={(x,y}: y=3x,y∈R} and B={{x,y}:y=x,x,y∈R} then which of the following is true?
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
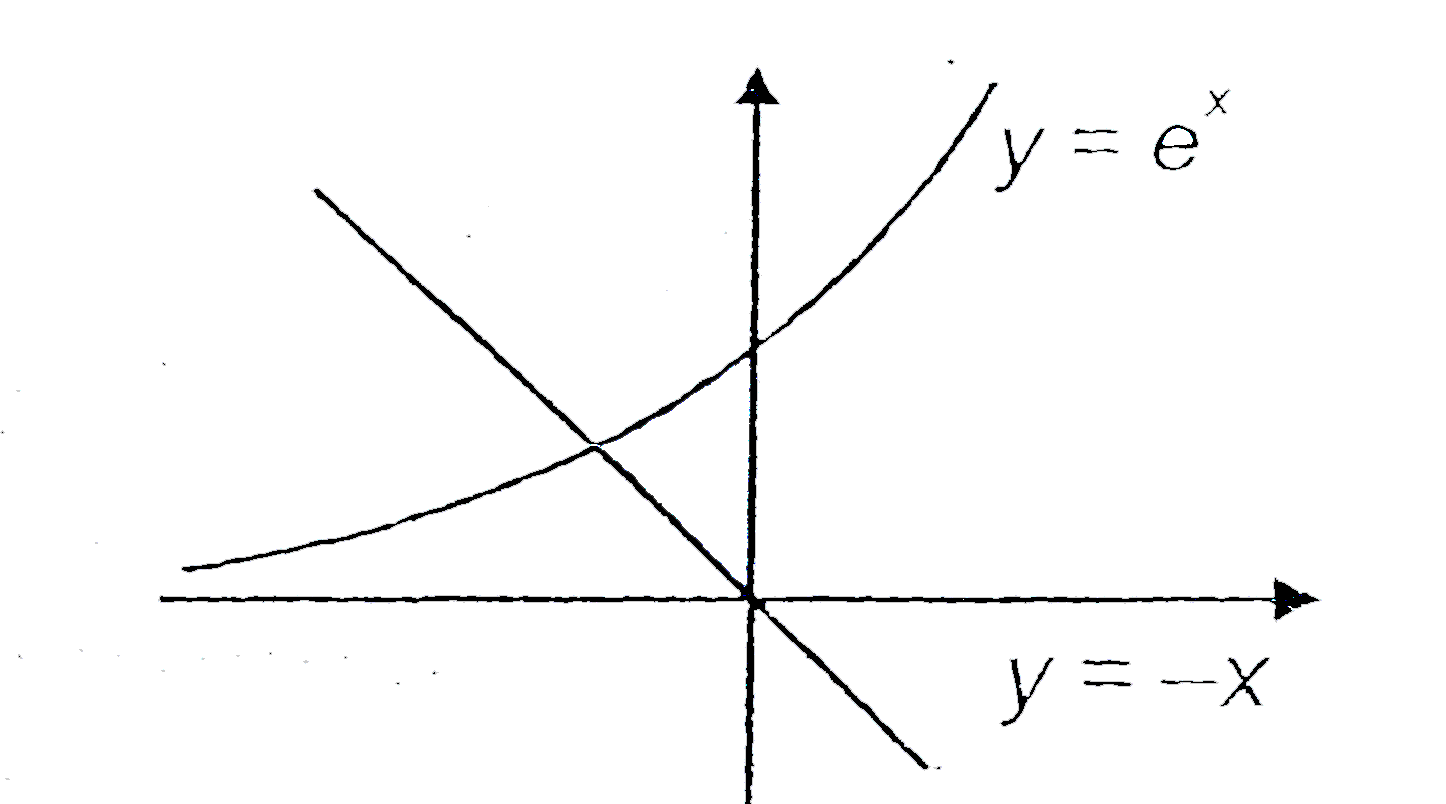
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View SolutionIf the sets A and B are defined are defined as A={(x,y):y=ex,x∈R},B={(x,y):y=x,x∈R}then
View SolutionWhich one of the following is not a function? {(x,y):x,y∈R,x2=y} b. {(x,y):x,y∈R,y2=x} c. {(x,y):x,y∈R,x=y3} d. {(x,y):x,y∈R,y=x3}
View Solution
