If p1,p2,p3 are respectively the perpendicular from the vertices of a triangle to the opposite sides, then find the value of p1p2p3.
a2b2c2R2
a2b2c24R2
4a2b2c3R2
a2b2c28R2
The correct Answer is:D
To find the value of p1p2p3, where p1,p2,p3 are the perpendiculars from the vertices of a triangle to the opposite sides, we can follow these steps:
Step 1: Understand the Triangle and Define the Perpendiculars
Let △ABC be a triangle with sides a,b,c opposite to vertices A,B,C respectively. The perpendiculars from vertices A,B,C to the opposite sides are denoted as p1,p2,p3.
Step 2: Express the Area of the Triangle
The area Δ of triangle ABC can be expressed in terms of the base and height. For each vertex, we can express the area as:
- From vertex B:
Δ=12×b×p1⟹p1=2Δb
- From vertex C:
Δ=12×c×p2⟹p2=2Δc
- From vertex A:
Δ=12×a×p3⟹p3=2Δa
Step 3: Multiply the Expressions for p1,p2,p3
Now, we can multiply these three equations:
p1p2p3=(2Δb)(2Δc)(2Δa)
This simplifies to:
p1p2p3=8Δ3abc
Step 4: Relate Area to Circumradius
We know from triangle properties that the area Δ can also be expressed in terms of the circumradius R:
Δ=abc4R
Substituting this into the equation for p1p2p3:
p1p2p3=8(abc4R)3abc
Step 5: Simplify the Expression
Now, simplifying the expression:
p1p2p3=8⋅a3b3c364R3abc=8a2b2c264R3=a2b2c28R3
Final Result
Thus, the value of p1p2p3 is:
p1p2p3=a2b2c28R3
Let △ABC be a triangle with sides a,b,c opposite to vertices A,B,C respectively. The perpendiculars from vertices A,B,C to the opposite sides are denoted as p1,p2,p3.
The area Δ of triangle ABC can be expressed in terms of the base and height. For each vertex, we can express the area as:
- From vertex B:
Δ=12×b×p1⟹p1=2Δb
- From vertex C:
Δ=12×c×p2⟹p2=2Δc
- From vertex A:
Δ=12×a×p3⟹p3=2Δa
Now, we can multiply these three equations:
p1p2p3=(2Δb)(2Δc)(2Δa)
This simplifies to:
p1p2p3=8Δ3abc
We know from triangle properties that the area Δ can also be expressed in terms of the circumradius R:
Δ=abc4R
Substituting this into the equation for p1p2p3:
p1p2p3=8(abc4R)3abc
Now, simplifying the expression:
p1p2p3=8⋅a3b3c364R3abc=8a2b2c264R3=a2b2c28R3
Thus, the value of p1p2p3 is:
p1p2p3=a2b2c28R3
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test55videos
PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEM
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type13videos
PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEM
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test31videos
PLANE AND STRAIGHT LINE IN SPACE
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test58videos
REAL FUNCTIONS
Similar Questions
If p1,p2,p3 are respectively the perpendiculars from the vertices of a triangle to the opposite sides , then cosAp1+cosBp2+cosCp3 is equal to
View SolutionIf p1,p2,p3 are the perpendiculars from the vertices of a triangle to the opposite sides, then prove that
p1p2p3=a2b2c28R3View Solution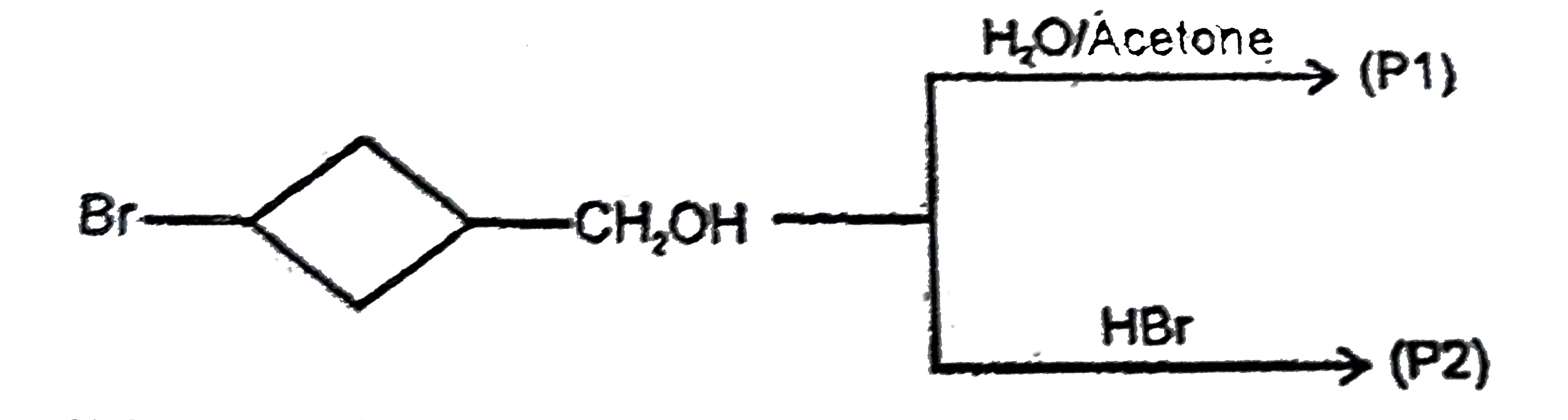
P1 and P2 are respectively :View SolutionIf the lengths of the perpendiculars from the vertices of a triangle ABC on the opposite sides are p1,p2,p3 then prove that 1p1+1p2+1p3=1r=1r1+1r2+1r3.
View SolutionLet A be a point inside a regular polygon of 10 sides. Let p1,p2....,p10 be the distances of A from the sides of the polygon. If each side is of length 2 units, then find the value of p1+p2+...+p10
View SolutionIf p1,p2,p3 are altitudes of a triangle ABC from the vertices A,B,C and △ the area of the triangle, then p−21+p−22+p−23 is equal to
View SolutionP1,P2,P3 are altitudes of a triangle ABC from the vertices A, B, C and Δ is the area of the triangle,
The value of P−11+P−12+P−13 is equal to-View SolutionIf p1,p2,p3 are the altitues of a triangle from the vertieces A,B,C and Δ is the area of the triangle then prove that
1p1+1p2−1p3=2ab(a+b+c)Δcos2C2View SolutionFind the value of :
12p2×4p2q×(−3p)View SolutionIf p2−p+1=0, then the value of p3n can be
View Solution

