If p1,p2,p3 are respectively the perpendiculars from the vertices of a triangle to the opposite sides , then cosAp1+cosBp2+cosCp3 is equal to
1/r
1/R
1/!
none of these
The correct Answer is:B
To solve the problem, we need to find the value of the expression:
cosAp1+cosBp2+cosCp3
where p1,p2,p3 are the perpendiculars from the vertices of triangle ABC to the opposite sides.
Step 1: Understanding the Perpendiculars
The perpendiculars p1,p2,p3 can be expressed in terms of the area Δ of triangle ABC and the sides a,b,c opposite to angles A,B,C respectively:
p1=2Δa,p2=2Δb,p3=2Δc
Step 2: Substitute the Perpendiculars
Now, substituting these expressions into our original equation:
cosAp1=cosA⋅a2Δ,cosBp2=cosB⋅b2Δ,cosCp3=cosC⋅c2Δ
Thus, we can rewrite the expression as:
cosA⋅a2Δ+cosB⋅b2Δ+cosC⋅c2Δ
Step 3: Combine the Terms
Combining these terms gives:
12Δ(acosA+bcosB+ccosC)
Step 4: Use the Sine Rule
Using the sine rule, we know that:
asinA=bsinB=csinC=2R
where R is the circumradius of triangle ABC. Therefore, we can express a,b,c in terms of R and the sines of the angles:
a=2RsinA,b=2RsinB,c=2RsinC
Step 5: Substitute Back into the Expression
Substituting these back into our expression:
acosA+bcosB+ccosC=2RsinAcosA+2RsinBcosB+2RsinCcosC
Using the identity sinAcosA=12sin2A:
=2R(12sin2A+12sin2B+12sin2C)=R(sin2A+sin2B+sin2C)
Step 6: Final Expression
Now substituting this back into our earlier expression:
12Δ⋅R(sin2A+sin2B+sin2C)
Step 7: Area of Triangle
The area Δ can also be expressed in terms of R:
Δ=abc4R
Thus, we can simplify our expression further:
R(sin2A+sin2B+sin2C)2⋅abc4R=2R2(sin2A+sin2B+sin2C)abc
Conclusion
After simplifying, we find that:
cosAp1+cosBp2+cosCp3=1R
Thus, the final answer is:
1R
The perpendiculars p1,p2,p3 can be expressed in terms of the area Δ of triangle ABC and the sides a,b,c opposite to angles A,B,C respectively:
Now, substituting these expressions into our original equation:
Combining these terms gives:
Using the sine rule, we know that:
Substituting these back into our expression:
Now substituting this back into our earlier expression:
The area Δ can also be expressed in terms of R:
After simplifying, we find that:
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
58 Videos
Similar Questions
If p1,p2,p3 are respectively the perpendicular from the vertices of a triangle to the opposite sides, then find the value of p1p2p3.
View SolutionIf p1,p2,p3 are the perpendiculars from the vertices of a triangle to the opposite sides, then prove that
p1p2p3=a2b2c28R3
View SolutionThe value of cosAP1+cosBP2+cosCP3 is
View SolutionIf the lengths of the perpendiculars from the vertices of a triangle ABC on the opposite sides are p1,p2,p3 then prove that 1p1+1p2+1p3=1r=1r1+1r2+1r3.
View Solution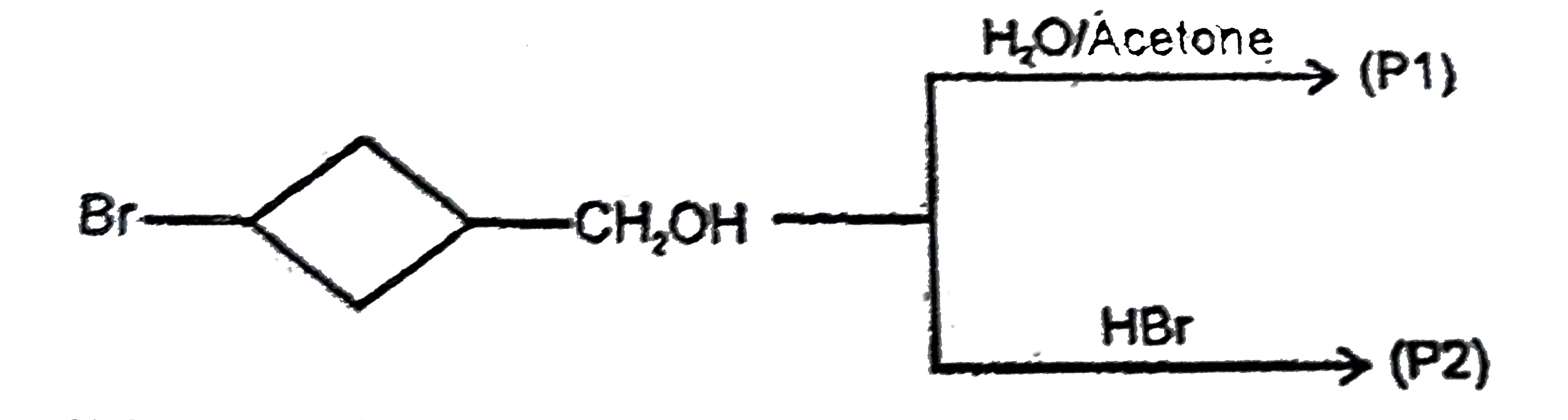
P1 and P2 are respectively :
View SolutionIf p1,p2,p3 are altitudes of a triangle ABC from the vertices A,B,C and △ the area of the triangle, then p−21+p−22+p−23 is equal to
View SolutionIf p1,p2 and p3 are the altitudes of a triangle from the vertices of a ΔABC and Δ is the area of triangle, prove that : 1p1+1p2−1p3=2ab(a+b+c)Δcos2.C2
View SolutionIf p1,p2,p3 are the altitues of a triangle from the vertieces A,B,C and Δ is the area of the triangle then prove that
1p1+1p2−1p3=2ab(a+b+c)Δcos2C2
View SolutionIf p1,p2,p3 are altitudes of a triangle ABC from the vertices A,B,C and! the area of the triangle, then p1.p2,p3 is equal to
View SolutionIf p1,p2,p3 re the altitudes of the triangle ABC from the vertices A, B and C respectivel. Prove that cosAp1+cosBp2+cosCp3=1R
View Solution
