Use isometric dot paper to sketch a rectangular prism with length 4 units, height 2 units and width 3 units.
To sketch a rectangular prism with length 4 units, height 2 units, and width 3 units on isometric dot paper, follow these steps:
1. Prepare the Isometric Dot Paper:
- Start with a sheet of isometric dot paper, which has a grid of dots arranged in a triangular pattern.
2. Draw the Base of the Prism:
- Begin by drawing a parallelogram to represent the base of the rectangular prism.
- For the length of 4 units, count 4 dots horizontally.
- For the width of 3 units, count 3 dots diagonally downwards from the right endpoint of the base line.
3. Complete the Parallelogram:
- From the endpoints of the 4-unit line, draw two lines that are parallel to the width line (3 units). These lines should be drawn diagonally upwards.
- Connect the endpoints of these two lines to complete the base shape, which is a parallelogram.
4. Draw the Vertical Edges:
- From each corner of the parallelogram, draw vertical lines upwards to represent the height of the prism.
- Each vertical line should be 2 units long, which means you will count 2 dots vertically from each corner.
5. Connect the Top Edges:
- Once the vertical lines are drawn, connect the tops of the vertical lines to complete the top face of the prism.
- This involves drawing lines between the tops of the vertical edges that correspond to the shape of the base.
6. Finalize the Prism:
- Ensure all lines are straight and connected properly to form a complete rectangular prism.
- You can darken the lines to make the shape more visible.
- Start with a sheet of isometric dot paper, which has a grid of dots arranged in a triangular pattern.
- Begin by drawing a parallelogram to represent the base of the rectangular prism.
- For the length of 4 units, count 4 dots horizontally.
- For the width of 3 units, count 3 dots diagonally downwards from the right endpoint of the base line.
- From the endpoints of the 4-unit line, draw two lines that are parallel to the width line (3 units). These lines should be drawn diagonally upwards.
- Connect the endpoints of these two lines to complete the base shape, which is a parallelogram.
- From each corner of the parallelogram, draw vertical lines upwards to represent the height of the prism.
- Each vertical line should be 2 units long, which means you will count 2 dots vertically from each corner.
- Once the vertical lines are drawn, connect the tops of the vertical lines to complete the top face of the prism.
- This involves drawing lines between the tops of the vertical edges that correspond to the shape of the base.
- Ensure all lines are straight and connected properly to form a complete rectangular prism.
- You can darken the lines to make the shape more visible.
Topper's Solved these Questions
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - TRY THIS
5 Videos
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - THINK AND DISCUSS
18 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
Similar Questions
The adjacent figure shows a rectangular prism of length l units, width w units and height h units.
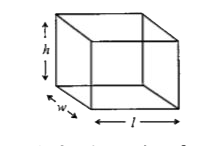
The formula for the total surface area of the rectangular prism is
View SolutionThe area of the largest triangle that can be fitted into a rectangle of the length L units and width B unit will be .........unit2 .
View Solution
Knowledge Check
Two circles with centres at A and B touch each other externally at T. Let BD is the tangent at D and TC is a common tangent. If AT has length 3 units and BT has length 2 units, then the length (in units ) of CB is
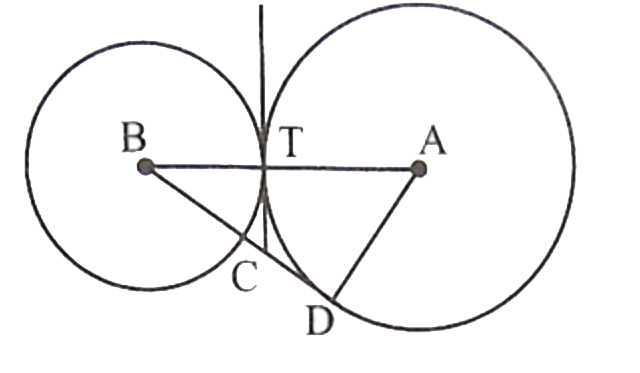 A43B52C53D74
A43B52C53D74In a trapezium, the two non-parallel sides are equal in length, each being of 5 units. The parallel sides are at a distance of 3 units apart. If the smaller side of the parallel sides is of length 2 units, then the sum of the diagonals of the trapezium is
A10√5 unitsB6√5 unitsC5√5 unitsD3√5 units
What is the area of the largest triangle that can be fitted into a rectangle of length l units and width w units?
View SolutionThe area of a rectangle gets reduced by 9 square units if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 squ units. Find the dimensions of the rectangle.
View SolutionThe ratio of length to width of a rectangular sheet of paper is 5:3. If the width of the sheet is 18 cm, find its length.
View SolutionThe area of a rectangle gets reduced by 9 square units if its length is reduced by 5 units and the breadth is increased by 3 units. If we increase the length by 3 units and breadth by 2 units, the area is increased by 67 square units. Find the length and breadth of the rectangle.
View SolutionA right pyramid has an equilateral triangular base of side 4 units. If the number of square units of its whole surface area is three times the number of cubic units of its volume, find its height. (a) 3 units (b) 4 units (c) 5 units (d) 6 units
View SolutionFind the volume of a rectangular box having a length of 5 m, width of 3 m , and height of 4 m .
View Solution
