The position vectors of two identical particles with respect to the origin in three-dimensional coordinate system are r1 and r2. The position vector of centre of mass of the system is given by
r1+r2
2(r1+r2)
r1−r2
r1+r22
The correct Answer is:D
Given, position vector of the first particle =r1
Position vector of second particle =r2
We know that,
Centre of mass of system
=m1r1×m2r2m1+m2
=mr1+mr2m+m
=m(r1+r2)2m=r1+r22
Similar Questions
Knowledge Check
The position Vectors of two identical particles with respect to the origin in the three-dimensional coordinator system are r1andr2 The position of the centre of mass of the system is given by
Ar1+r2B2(r1+r2)Cr1−r2Dr1+r22A system of two identical, uniform discs with identical circular cavities, is shown in the figure. Different relevant coordinates are given in the figure. The coordinates of the centre of mass of the system are
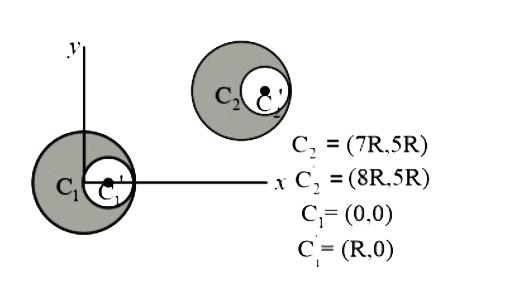 A(3R2,5R4)B(19R6,5R2)C(R6,R4)D(20R6,5R2)
A(3R2,5R4)B(19R6,5R2)C(R6,R4)D(20R6,5R2)
Obtain an expression for the position vector of centre of mass of a system of n particles.
View SolutionWhat is the position vector of centre of mass of two particles of equal masses ?
View SolutionObtain an expression for the position vector of centre of mass of a two particle system.
View SolutionThe position vector of a particle with respect to origin "0" is →r.If the torque acting on the particle is zero,then
View SolutionStatement-1 : The centre of mass of a system of n particles is the weighted average of the position vector of the n particles making up the system
. Statement-2 : The position of the centre of mass of a system is independent of coordinate system
View SolutionA system of two identical, uniform discs with identical circular cavities, is shown in the figure. Different relevant coordinates are given in the figure. The coordinates of the centre of mass of the system are

View Solution
