The position Vectors of two identical particles with respect to the origin in the three-dimensional coordinator system are r1andr2 The position of the centre of mass of the system is given by
(a)r1+r2
(b)2(r1+r2)
(c)r1−r2
(d)r1+r22
The correct Answer is:D
To find the position of the center of mass of two identical particles with position vectors r1 and r2, we can follow these steps:
1. Identify the Given Information:
- The position vectors of the two identical particles are given as r1 and r2.
- Since the particles are identical, we denote their masses as m1=m and m2=m.
2. Use the Formula for Center of Mass:
- The formula for the position vector of the center of mass R of a system of particles is given by:
R=m1r1+m2r2m1+m2
3. Substitute the Masses:
- Since both particles have the same mass m, we can substitute m1 and m2 in the formula:
R=mr1+mr2m+m
4. Simplify the Expression:
- Factor out the mass m from the numerator:
R=m(r1+r2)2m
- The mass m in the numerator and denominator cancels out:
R=r1+r22
5. Conclusion:
- The position vector of the center of mass of the two identical particles is:
R=r1+r22
- The position vectors of the two identical particles are given as r1 and r2.
- Since the particles are identical, we denote their masses as m1=m and m2=m.
- The formula for the position vector of the center of mass R of a system of particles is given by:
R=m1r1+m2r2m1+m2
- Since both particles have the same mass m, we can substitute m1 and m2 in the formula:
R=mr1+mr2m+m
- Factor out the mass m from the numerator:
R=m(r1+r2)2m
- The mass m in the numerator and denominator cancels out:
R=r1+r22
- The position vector of the center of mass of the two identical particles is:
R=r1+r22
Similar Questions
Knowledge Check
Which of the following points is the likely position of the centre of mass of the system shown in Fig.
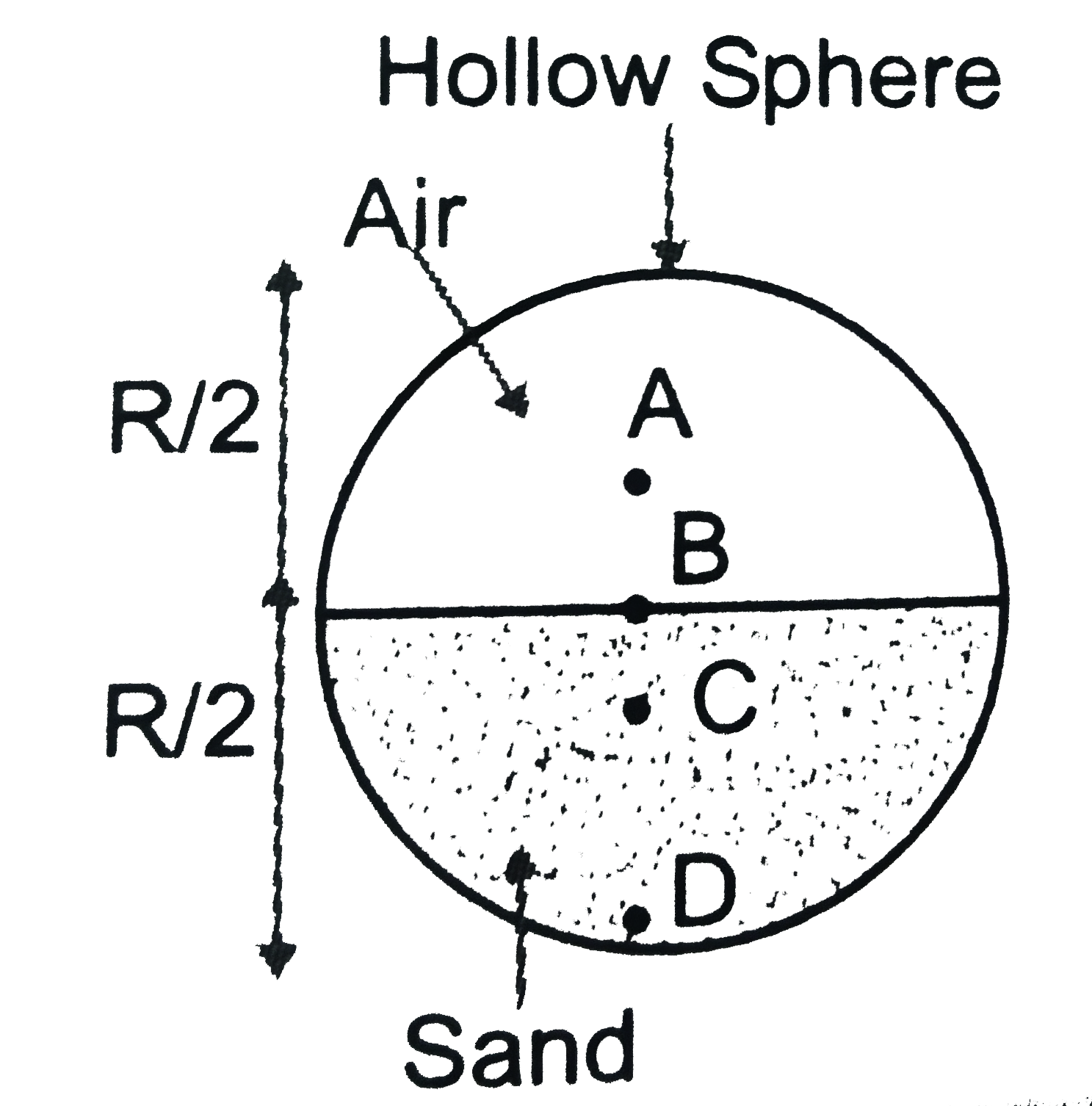 AABBCCDD
AABBCCDD
Which of the following points is the likely position of the centre of mass of the system shown in Fig.

View SolutionThe position of center of mass of a system of particles does not depend upon the
View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View SolutionA system of two identical, uniform discs with identical circular cavities, is shown in the figure. Different relevant coordinates are given in the figure. The coordinates of the centre of mass of the system are
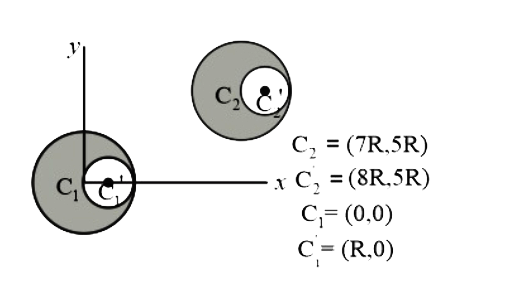
View SolutionA system of two identical, uniform discs with identical circular cavities, is shown in the figure. Different relevant coordinates are given in the figure. The coordinates of the centre of mass of the system are

View SolutionFour identical particles each of mass m are arranged at the corners of a square of sie a. If mass of one of th particle is doubled, the shift in the centre of mass of the system is
View SolutionA large number of particles are placed around the origin, each at a distance R from the origin. The distance of the center of mass of the system from the origin is
View Solution