A current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-z plane. If the current in the loop is i. The resultant magnetic field due to the two semicircular parts at their common centre is
μ0i2√2R
μ0i2R
μ0i4R
μ0i√2R
The correct Answer is:A
The loop mentioned in the question must look like one as shown in the figure
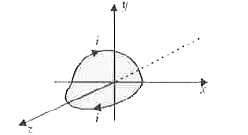
Magnetic field at the centre due to semicircular loop lying in x-y plane, Bxy=12(μ0i2R) negative z direction.
Similarly , field due to loop in x-z plane, Bxz=12(μ0i2R) in negative y direction.
∴ Magnitude of resultant magnetic field.
B=√B2xy+B2xz=√(μ0i4R)+(μ0i4R)2=μ0i4R√2=μ0i2√2R
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - CHECK YOUR NEET VITALS
25 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - AIPMT/NEET (MCQ.s)
34 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
Similar Questions
A current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-z plane. If the current in the loop is i, the resultant magnetic field due to two semicircular parts at their common centre is
View SolutionA current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude to →B at the origin.
View Solution
Knowledge Check
A current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-y plane. If the current in the loop is i, the resultant magnetic field due to two semicircular parts at their common centre is
Aμ0i2√2RBμ0i2RCμ0i4RDμ0i√2RA current I, flowing in a long and straight wire along z-axis, is directed into two identical semicircular portions lying in y-z and x-z planes as shown in the figure. The magnetic field at the centre O is
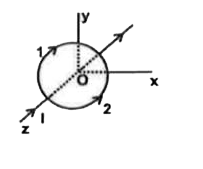 AzeroBμ0l4πCμ0l2√2rDμ0l√2r
AzeroBμ0l4πCμ0l2√2rDμ0l√2rIn Fig ABCDEFA was a square loop of side l, but is folded in two equal parts so that half of it lies in the x-z plane and the other half lies in the y-z plane. The origin O is centre of the frame also. The loop carries current 'i'. The magnetic field at the centre is
 Aμ0i2√2πl(ˆi−ˆj)Bμ0i4πl(−ˆi−ˆj)C√2μ0iπl(ˆi+ˆj)Dμ0i√2πl(ˆi+ˆj)
Aμ0i2√2πl(ˆi−ˆj)Bμ0i4πl(−ˆi−ˆj)C√2μ0iπl(ˆi+ˆj)Dμ0i√2πl(ˆi+ˆj)
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude to →B at the origin.
View SolutionA current I, flowing in a long and straight wire along z-axis, is directed into two identical semicircular portions lying in y-z and x-z planes as shown in the figure. The magnetic field at the centre O is

View SolutionIn Fig ABCDEFA was a square loop of side l, but is folded in two equal parts so that half of it lies in the x-z plane and the other half lies in the y-z plane. The origin O is centre of the frame also. The loop carries current 'i'. The magnetic field at the centre is

View SolutionA circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
View SolutionTwo similar coils of radius R are lying concentrically with their planes at right angles to each other. The currents flowing in them are I and 2I, respectively. The resultant magnetic field induction at the centre will be
View Solution
