A current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in x-z plane. If the current in the loop is i, the resultant magnetic field due to two semicircular parts at their common centre is
The correct Answer is:D
To solve the problem of finding the resultant magnetic field at the common center of two identical semicircular current loops, we can follow these steps:
Step 1: Understand the Configuration
We have two semicircular loops:
- One semicircular loop lies in the x-y plane.
- The other semicircular loop lies in the x-z plane.
Both loops have the same radius R and carry the same current I.
Step 2: Determine the Magnetic Field from Each Semicircular Loop
The magnetic field B at the center of a semicircular loop carrying current I is given by the formula:
B=μ0I4R
where μ0 is the permeability of free space.
Step 3: Calculate the Magnetic Field from the Semicircle in the x-y Plane
For the semicircular loop in the x-y plane, the magnetic field Bxy at the center (common center) will point in the negative z-direction (using the right-hand rule):
Bxy=μ0I4R(in the -z direction)
Step 4: Calculate the Magnetic Field from the Semicircle in the x-z Plane
For the semicircular loop in the x-z plane, the magnetic field Bxz at the center will point in the negative y-direction:
Bxz=μ0I4R(in the -y direction)
Step 5: Combine the Magnetic Fields
The two magnetic fields Bxy and Bxz are perpendicular to each other. To find the resultant magnetic field B, we can use the Pythagorean theorem:
B=√B2xy+B2xz
Substituting the values:
B=√(μ0I4R)2+(μ0I4R)2
B=√2(μ0I4R)2
B=μ0I4R√2
Step 6: Final Result
Thus, the resultant magnetic field B at the common center of the two semicircular loops is:
B=μ0I2√2R
Conclusion
The resultant magnetic field at the common center of the two semicircular parts is:
μ0I2√2R
We have two semicircular loops:
- One semicircular loop lies in the x-y plane.
- The other semicircular loop lies in the x-z plane.
Both loops have the same radius R and carry the same current I.
The magnetic field B at the center of a semicircular loop carrying current I is given by the formula:
B=μ0I4R
where μ0 is the permeability of free space.
For the semicircular loop in the x-y plane, the magnetic field Bxy at the center (common center) will point in the negative z-direction (using the right-hand rule):
Bxy=μ0I4R(in the -z direction)
For the semicircular loop in the x-z plane, the magnetic field Bxz at the center will point in the negative y-direction:
Bxz=μ0I4R(in the -y direction)
The two magnetic fields Bxy and Bxz are perpendicular to each other. To find the resultant magnetic field B, we can use the Pythagorean theorem:
B=√B2xy+B2xz
Substituting the values:
B=√(μ0I4R)2+(μ0I4R)2
B=√2(μ0I4R)2
B=μ0I4R√2
Thus, the resultant magnetic field B at the common center of the two semicircular loops is:
B=μ0I2√2R
The resultant magnetic field at the common center of the two semicircular parts is:
μ0I2√2R
Similar Questions
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude to →B at the origin.
View SolutionIn Fig ABCDEFA was a square loop of side l, but is folded in two equal parts so that half of it lies in the x-z plane and the other half lies in the y-z plane. The origin O is centre of the frame also. The loop carries current 'i'. The magnetic field at the centre is

View Solution
Knowledge Check
A 4 A current carrying loop consists of three identical quarter circles of radius 5 cm lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin joined together, value of B at the origin is
Aμ010(ˆi+ˆj−ˆk)TBμ010(−ˆi+ˆj+ˆk)TCμ05(ˆi+ˆj+ˆk)TD10μ0(ˆi+ˆj+ˆk)T
Two identical coils have· a common centre and their planes are at right angles to each other and carry equal currents. If the magnitude of the induction field at the centre due to one of the coil is 'B ', then the resultant magnetic induction field due to combination at their common centre is
View SolutionA current I, flowing in a long and straight wire along z-axis, is directed into two identical semicircular portions lying in y-z and x-z planes as shown in the figure. The magnetic field at the centre O is
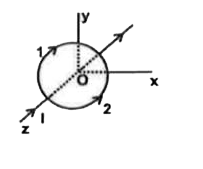
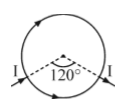
View SolutionA current I enters a uniform circular coil of radius R, branches into two parts and then recombines as shown in the circuit diagram. The resultant magnetic field at the centre of the coil is :
View SolutionConsider a circular loop of wire lying in the plane of the table. Let the current pass through the loop clockwise. Apply the right hand rule out the direction of magnetic field inside and outside the loop.
View SolutionTwo similar circular loops of radius R are lying concentrically with their planes at right angles to each other. The currents flowing in them are I and I√3 respectively. The magnetic field at the centre of the coil is
View SolutionTwo similar coils of radius R are lying concentriclaly with their planes at right angels to each other. The currents flowing in them are I and 2I respectively. The resulant magntic field induction at the centre will be
View SolutionTwo identical coils carry equal currents have a common centre and their planes are at right angles to each other. The ratio of the magnitude of the resulatant magnetic field at the centre and the field due to one coil is
View Solution
