In the adjoining figure, AB||CD. If the ∠BAE=25∘and∠CDE=30∘, then find ∠AED
The correct Answer is:55∘
To solve the problem step by step, we will use the properties of parallel lines and angles.
Step 1: Identify the Given Information
We are given that:
- Lines AB and CD are parallel (AB || CD).
- Angle BAE = 25°.
- Angle CDE = 30°.
Step 2: Draw a Construction
To find angle AED, we will draw a line PE that is parallel to AB and CD, passing through point E. This helps us to use the properties of alternate interior angles.
Step 3: Identify Angles Using Alternate Interior Angles
Since AB is parallel to PE:
- Angle BAE (25°) is equal to angle AEP (let's call this angle 1).
Thus, we have:
- Angle AEP = 25° (by alternate interior angles).
Step 4: Identify Another Angle Using Alternate Interior Angles
Since PE is parallel to CD:
- Angle CDE (30°) is equal to angle PED (let's call this angle 2).
Thus, we have:
- Angle PED = 30° (by alternate interior angles).
Step 5: Calculate Angle AED
Now, angle AED can be found by adding angle AEP and angle PED:
- Angle AED = Angle AEP + Angle PED
- Angle AED = 25° + 30° = 55°.
Final Answer
Therefore, angle AED = 55°.
---
We are given that:
- Lines AB and CD are parallel (AB || CD).
- Angle BAE = 25°.
- Angle CDE = 30°.
To find angle AED, we will draw a line PE that is parallel to AB and CD, passing through point E. This helps us to use the properties of alternate interior angles.
Since AB is parallel to PE:
- Angle BAE (25°) is equal to angle AEP (let's call this angle 1).
Thus, we have:
- Angle AEP = 25° (by alternate interior angles).
Since PE is parallel to CD:
- Angle CDE (30°) is equal to angle PED (let's call this angle 2).
- Angle PED = 30° (by alternate interior angles).
Now, angle AED can be found by adding angle AEP and angle PED:
- Angle AED = Angle AEP + Angle PED
- Angle AED = 25° + 30° = 55°.
Therefore, angle AED = 55°.
Topper's Solved these Questions
- LINES AND ANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINES AND ANGLESExercise:Revision Exercise (very Short Answer Questions )
Explore 10 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINES AND ANGLESExercise:Revision Exercise (short Answer Questions)
Explore 12 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINES AND ANGLESExercise:Exercise 6 B
Explore 16 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Revision Exercise
Explore 12 Videos
- NUMBER SYSTEMBook:NAGEEN PRAKASHAN ENGLISHChapter:NUMBER SYSTEMExercise:Revision Exercise (short Answer Questions)
Explore 10 Videos
Similar Questions
Knowledge Check
In the given figure, AB∣∣CD. Find the value of x
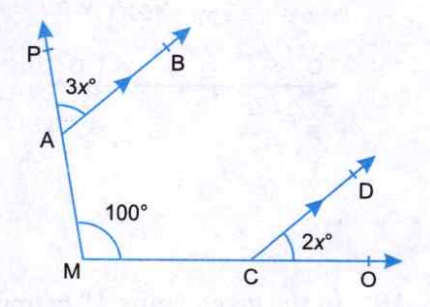 A20B25C40D60
A20B25C40D60
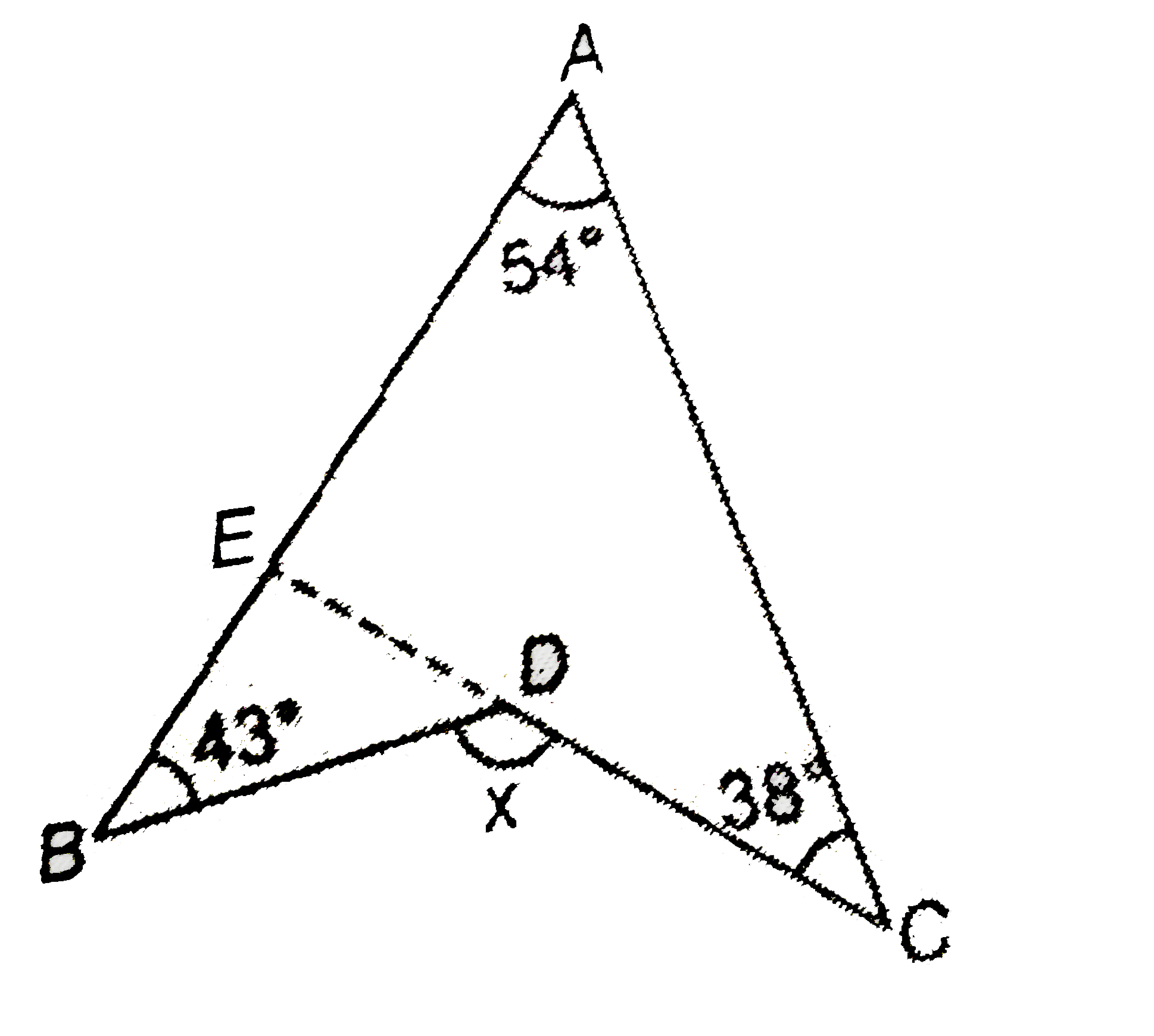
In the adjoining figure find ∠x
View SolutionIn the given figreu AB∣∣CD,∠BAD=30∘and∠ECD=50∘, find ∠CED
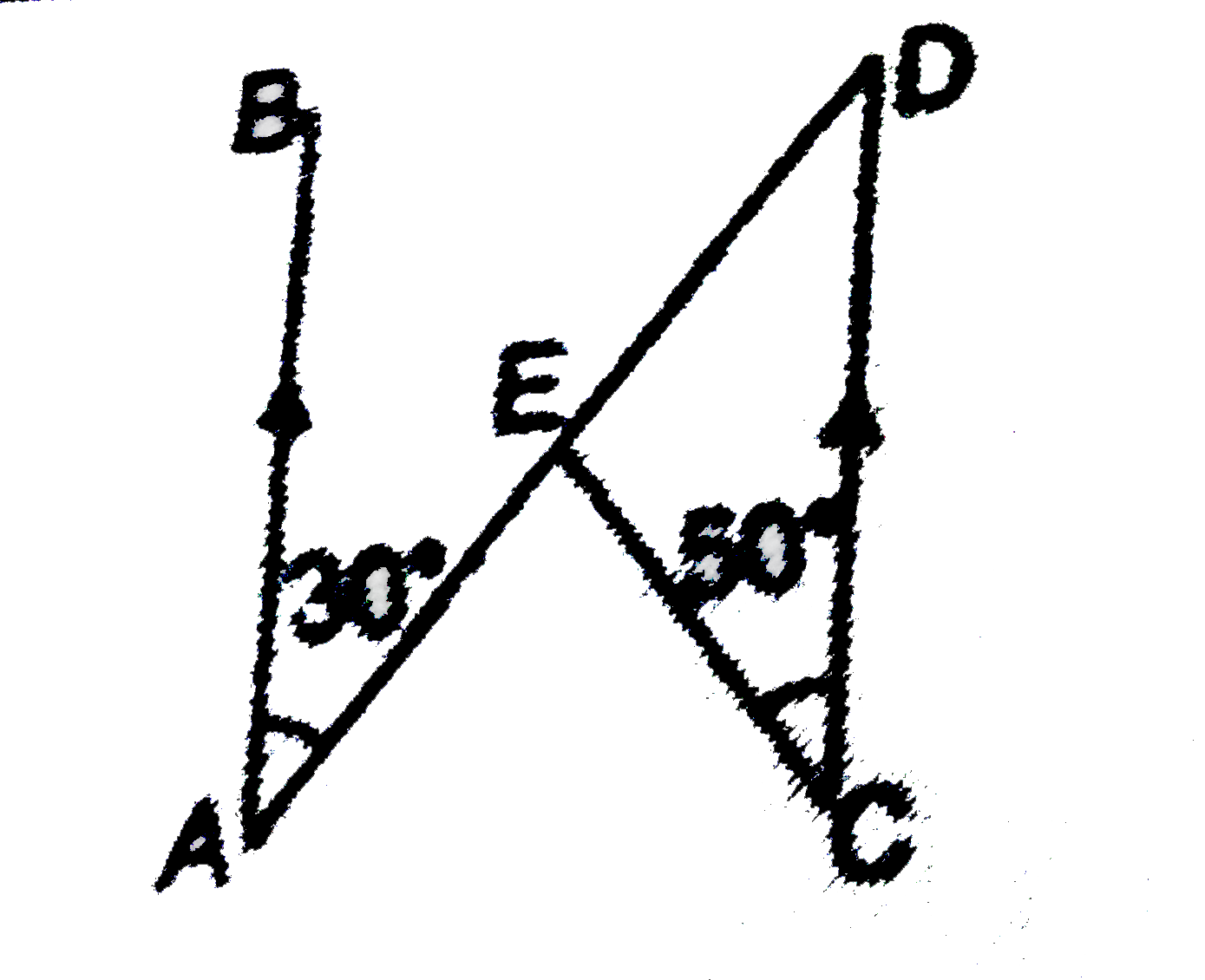
View SolutionIn the adjoining figure, ∠ABC=95∘ and ∠DAC=35∘, then find the value of ∠ACD.

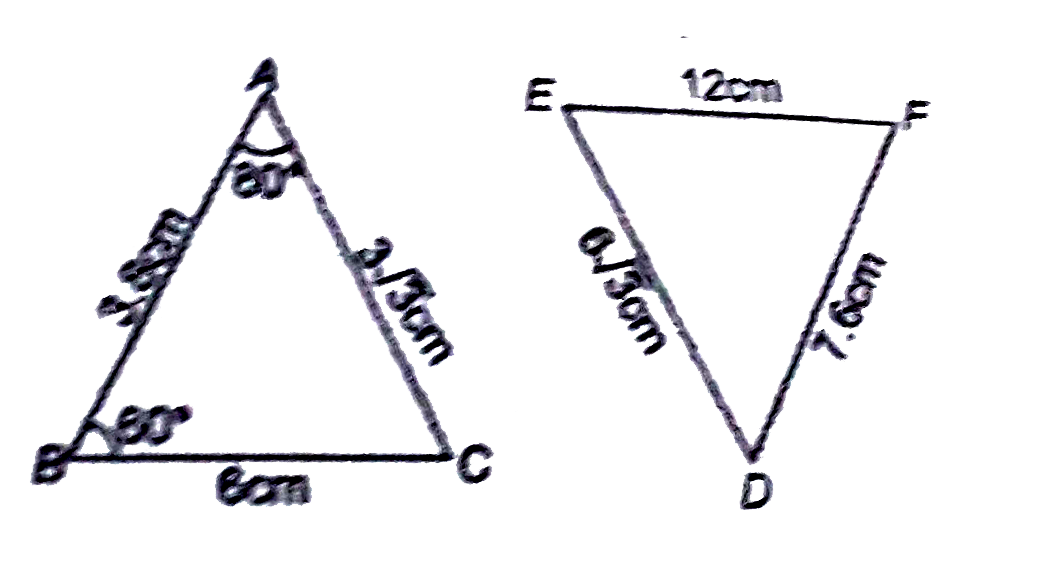
View SolutionIn the adjoining figure, find AC . (FIGURE)
View Solutionin the adjoining figure find ∠F.
View SolutionIn the adjoining figure, AB is a chord of the circle. If ∠AEB=110∘ and ∠EBC=25∘,then find the value of ∠ADB.
View SolutionIn the adjoining figure, p||q. Find the unknown angles.
View Solution