Bisectors of angles A and B of a parallelogram ABCD meet at point M. Prove that ∠AMB=12(∠C+∠D)
To prove that ∠AMB=12(∠C+∠D) in parallelogram ABCD where the angle bisectors of ∠A and ∠B meet at point M, we can follow these steps:
1. Understanding the Properties of a Parallelogram:
In a parallelogram, the sum of the interior angles is 360∘. Thus, we have:
∠A+∠B+∠C+∠D=360∘
2. Using the Angle Bisector Property:
Since AM and BM are angle bisectors, we can express the angles as:
∠A=2×∠1and∠B=2×∠2
where ∠1 and ∠2 are the angles formed by the bisectors.
3. Substituting into the Angle Sum Equation:
Substitute the expressions for ∠A and ∠B into the equation from step 1:
2∠1+2∠2+∠C+∠D=360∘
This simplifies to:
2(∠1+∠2)+∠C+∠D=360∘
Let's call this Equation (1).
4. Applying the Triangle Angle Sum Property:
In triangle AMB, the sum of the angles is:
∠1+∠2+∠AMB=180∘
Rearranging gives us:
∠1+∠2=180∘−∠AMB
Let's call this Equation (2).
5. Substituting Equation (2) into Equation (1):
Substitute ∠1+∠2 from Equation (2) into Equation (1):
2(180∘−∠AMB)+∠C+∠D=360∘
This expands to:
360∘−2∠AMB+∠C+∠D=360∘
6. Simplifying the Equation:
Subtract 360∘ from both sides:
−2∠AMB+∠C+∠D=0
Rearranging gives:
2∠AMB=∠C+∠D
7. Final Result:
Dividing both sides by 2 yields:
∠AMB=12(∠C+∠D)
This completes the proof.
In a parallelogram, the sum of the interior angles is 360∘. Thus, we have:
∠A+∠B+∠C+∠D=360∘
Since AM and BM are angle bisectors, we can express the angles as:
∠A=2×∠1and∠B=2×∠2
where ∠1 and ∠2 are the angles formed by the bisectors.
Substitute the expressions for ∠A and ∠B into the equation from step 1:
2∠1+2∠2+∠C+∠D=360∘
This simplifies to:
2(∠1+∠2)+∠C+∠D=360∘
Let's call this Equation (1).
In triangle AMB, the sum of the angles is:
∠1+∠2+∠AMB=180∘
Rearranging gives us:
∠1+∠2=180∘−∠AMB
Let's call this Equation (2).
Substitute ∠1+∠2 from Equation (2) into Equation (1):
2(180∘−∠AMB)+∠C+∠D=360∘
This expands to:
360∘−2∠AMB+∠C+∠D=360∘
Subtract 360∘ from both sides:
−2∠AMB+∠C+∠D=0
Rearranging gives:
2∠AMB=∠C+∠D
Dividing both sides by 2 yields:
∠AMB=12(∠C+∠D)
This completes the proof.
Topper's Solved these Questions
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Revision Exercise (very Short Answer Questions )
10 Videos
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Revision Exercise (short Answer Questions)
12 Videos
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6 B
16 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Revision Exercise
12 Videos
- NUMBER SYSTEMBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - NUMBER SYSTEMEXERCISE - Revision Exercise (short Answer Questions)
10 Videos
Similar Questions
Bisectors of angles A and D of a quadrilateral ABCD meet at P. Prove that ∠APD=12(∠B+∠C)
View SolutionIn triangle ABC,the bisector of interior angle A and the bisector angle C meet at point O. Prove that ∠AOC=12∠B
View SolutionIn ΔABC, bisectors of ∠Band∠C interesct each other at point O. Prove that ∠BOC=90∘+12∠Ai.e.,∠1=90∘+12A
View SolutionIn ΔABC, bisectors of ∠Band∠C interesct each other at point O. Prove that ∠BOC=90∘+12∠Ai.e.,∠1=90∘+12
View SolutionIn triangle ABC , the internal bisector of ∠A∠Band∠C meet at point I . Prove that :
12(AB+BC+CA)<AI+BI+CI
View SolutionThe bisectors of angles A and B of a scalene triangle ABC meet at O.
What is the relation between angle ACO and angle BCO?
View SolutionIn the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD=90∘
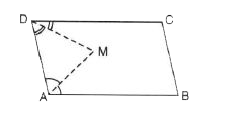
View SolutionIn the given figure, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that ∠AMD=90∘.
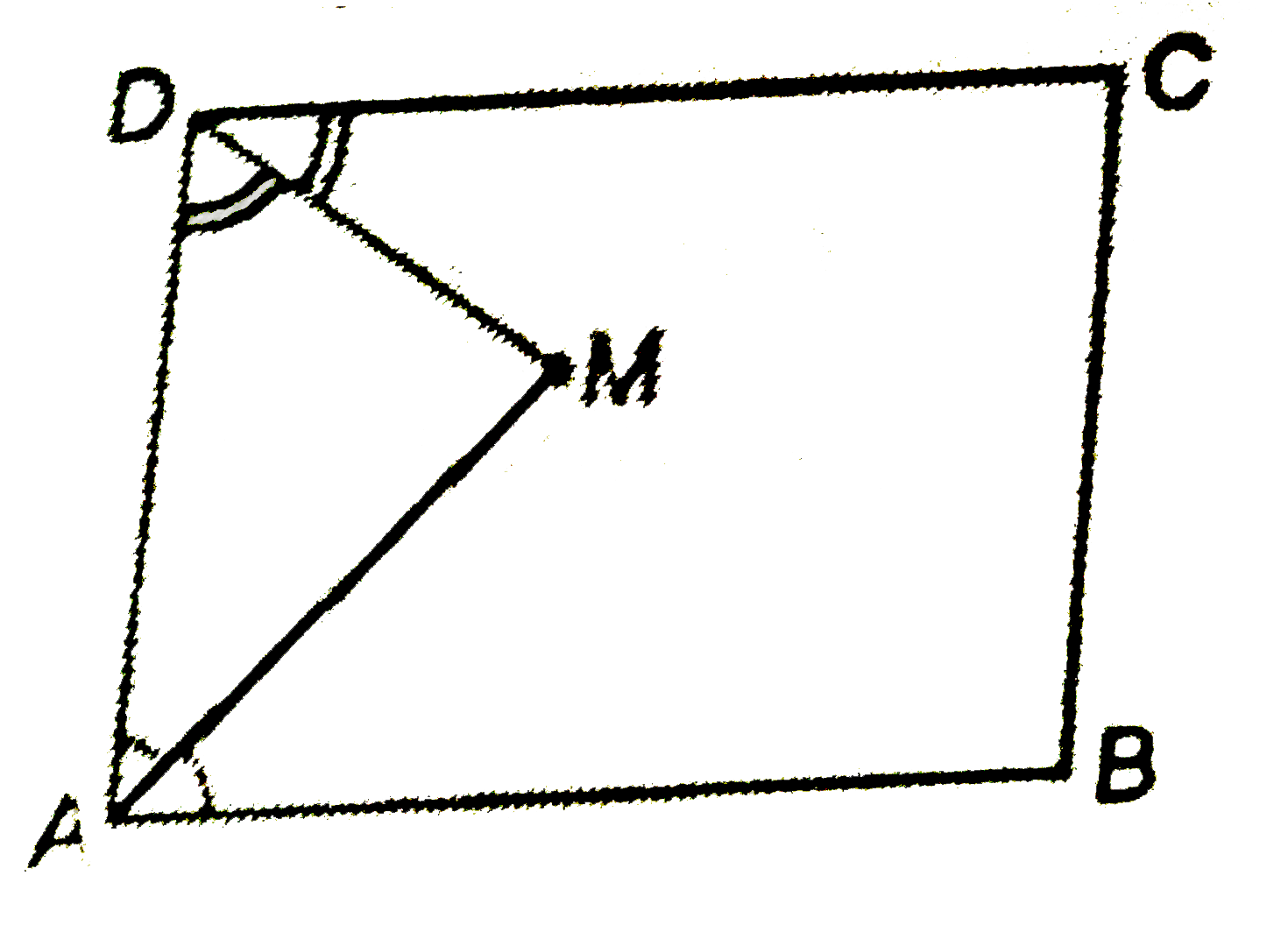
View SolutionIn a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
View SolutionShow that the bisectors of angles of a parallelogram form a rectangle.
View Solution
