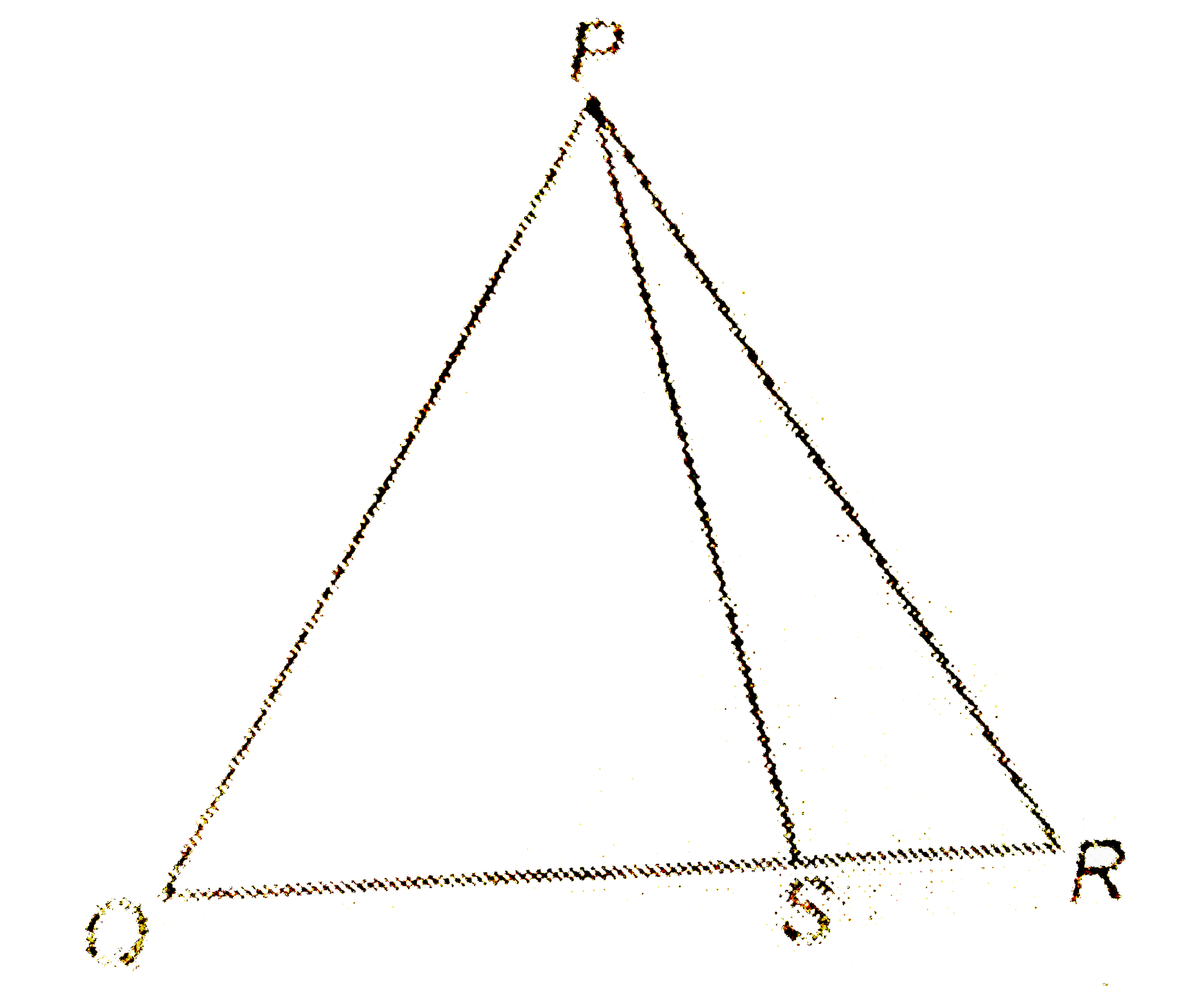
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Find the lengths of QR and PS.
Given : A point S on side QR of ΔPQR.
Tp prove : PQ+QR+RP>2PS
Proof : In ΔPQS, we have
PQ+QS>PS ...(1)
( ∵ sum of any sides of a triangle is greater than the third side)
Now, in ΔPSR, we have
RS+RP>PS ...(2)
( ∵ Sum of any two sides of a triangle is greater than the third side)
Adding (1) and (2), we get
PQ+QS+RS+RP>2PS
⇒PQ+QR+RP>2PS
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Prove ΔPQR~ΔSPR.
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

area of ΔPQRarea of ΔSPR
View SolutionS is any point on side QR of a ΔPQR. Show that PQ+QR+RP>2PS .
View SolutionIf Q is a point on the side SR of a triangle ΔPSR such that PQ=PR then prove that PS>PQ
View SolutionA circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths QM, RN and PL.
View SolutionA circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths QM, RN and PL.
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
View SolutionA and B are respectively the points on the sides PQ and PR of a ΔPQR such that PQ =12.5 cm, PA= 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reason for your answer.
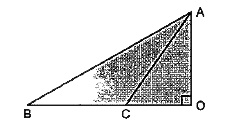
View SolutionIn triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC
View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View Solution
