ABCD is a square EF is parallel to BD. R is the mid-point of EF. Prove that :
(i) BE=DF
(ii) AR bisects angle BAD
(iii) If AR produced it will pass through C.

Step by step video & image solution for ABCD is a square EF is parallel to BD. R is the mid-point of EF. Prove that : (i) BE = DF (ii) AR bisects angle BAD (iii) If AR produced it will pass through C. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7b
17 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
In parallelogram ABCD, E is the mid-point of side AB and CE bisect angle BCD. Prove that :
(i) AE=AD
(ii) DE bisect ∠ADC and
(iii) Angle DEC is a right angle.
View SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
∠DXA=∠AYB
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

BC= BE
View SolutionIn Figure, O is the mid point of AB and CD . Prove that (i) AOC≅BOD (ii) AC=BD
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
CE bisects angle C
View SolutionIn ΔABC, AB = AC and the bisectors of angles B and C intersect at point O. Prove that :
(i) BO = CO
(ii) AO bisects angle BAC.
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).

View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

∠DEC=90∘
View SolutionIn a quadrilateral ABCD, AB = AD and CB = CD. Prove that :
(i) AC bisects angle BAD
(ii) AC is perpendicular bisector of BD.
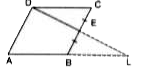
View SolutionFrom the given diagram, in which ABCD is a parallelgram, ABL is a line segment and E is mid point of BC. Prove that :
(i) ΔDCE≅ΔLBE
(ii) AB = BL
(iii) AL = 2DC
View Solution
