In quadrilateral ABCD, AB is the shortest side and DC is the longest side. Prove that :
(i) ∠B>∠D
(ii) ∠A>∠C
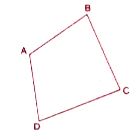
The correct Answer is:(i) ∠B>∠D (ii) ∠A>∠(C)
Step by step video & image solution for In quadrilateral ABCD, AB is the shortest side and DC is the longest side. Prove that : (i) angleB gt angleD (ii) angleA gt angleC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Revision Exercise (short Answer Type Question)
10 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Revision Exercise (long Answer Type Question)
8 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7b
17 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
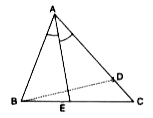
In the following diagram, AD = AB and AE bisects angle A. Prove that :
(i) BE = DE (ii) ∠ABD>∠C
View SolutionIn parallelogram ABCD, E is the mid-point of side AB and CE bisect angle BCD. Prove that :
(i) AE=AD
(ii) DE bisect ∠ADC and
(iii) Angle DEC is a right angle.
View SolutionIn a quadrilateral ABCD the linesegment bisecting ∠Cand∠D meet at E. Prove that ∠A+∠B=2∠CED.
View SolutionIn quadrilateral ABCD ,side DC is largest show that AB + AD > DC - BC
View SolutionIn quadrilateral ABCD, side AB is parallel to side DC. If ∠A:∠D=1:2and∠C:∠B=4:5.
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrialateral ABCD.
View SolutionIn the given figure, AB=CD and AD=CB. Prove that :
(i) ΔABD=ΔCDB
(ii) ∠A=∠C

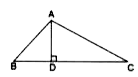
View SolutionFrom the following figure, prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
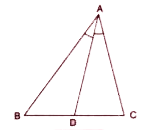
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC

View SolutionIn a quadrilateral ABCD, AB = AD and CB = CD. Prove that :
(i) AC bisects angle BAD
(ii) AC is perpendicular bisector of BD.
View Solution
