Construct a ΔABC in which AB = 5 cm, AC + BC = 8 cm and ∠B=60∘.
Steps of construction :
1. Draw AB = 5 cm.
2. Construct ∠ABP=60∘ and cut BP = 8 cm.
3. Join AP.
4. Draw the perpendicular bisector of AP which intersect BP at C.
5. Join AC.
∴ΔABC is the required triangle.
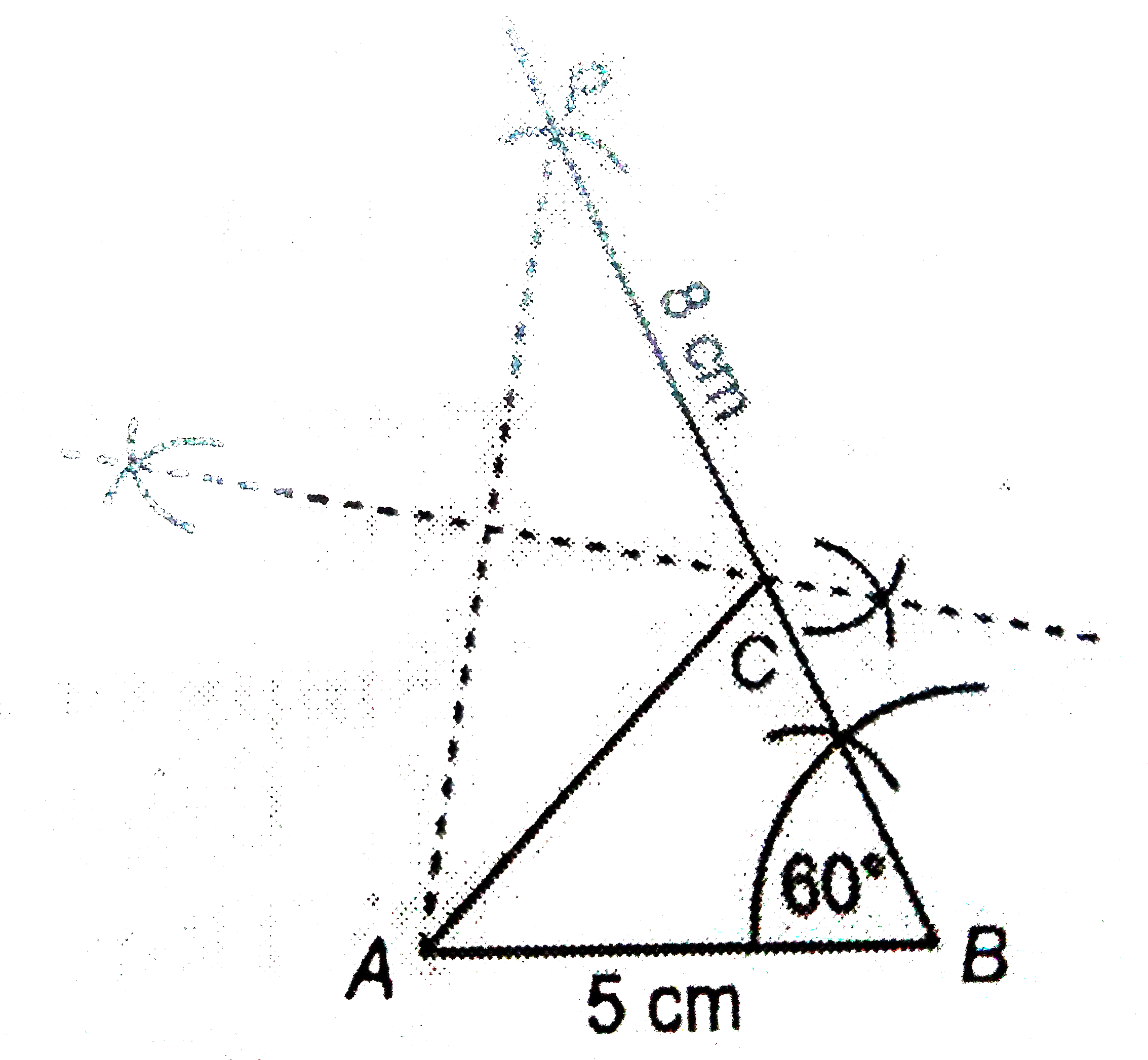
Topper's Solved these Questions
- CONSTRUCTIONSBook:NAGEEN PRAKASHAN ENGLISHChapter:CONSTRUCTIONSExercise:EXERCISE
Explore 36 Videos
- CO-ORDINATE GEOMETRY Book:NAGEEN PRAKASHAN ENGLISHChapter:CO-ORDINATE GEOMETRY Exercise:Exercise
Explore 8 Videos
- HERONS'S FORMULABook:NAGEEN PRAKASHAN ENGLISHChapter:HERONS'S FORMULAExercise:Revision Exercise
Explore 11 Videos
Similar Questions
Construct a ΔABC in which AB = 5 cm, AC = 4.5 cm and ∠A=60∘.
View SolutionConstruct a ΔABC in which AB = 6.3 cm, AC = 4.5 cm and ∠A=45∘.
View SolutionConstruct a ΔABC in which AB = 5 cm, BC = AC cm ∠A=60∘. Draw the perpendicular bisector of AB and BC. If these bisector intersect at O. Measure OA and OB.
View SolutionConstruct a ΔABC in which AB = 5 cm, ∠A=60∘ and ∠B=45∘. Draw the bisector of ∠A and ∠B. If these bisectors intersect at M. Measure CM.
View SolutionUse ruler and compasses only for this question
Construct ΔABC, where AB = 3.5 cm, BC= 6 cm and ∠ABC=60∘.
View SolutionConstruct a ΔABC in which BC = 5.5 cm, ∠B=60∘ and ∠C=75∘.
View SolutionConstruct a ΔABC with sides BC = 6 cm, AB = 5 cm and ∠ABC=60∘. Then construct a triangle whose sides are 34 of the corresponding sides of ΔABC.
View SolutionConstruct a ΔABC in which AB = 4 cm, BC = 5.2 cm and CA = 4.5 cm.
View SolutionConstruct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC=105∘. Hence
Construct the locus of points equidistant from BA and BC.
View SolutionConstruct an isosceles ΔABC in which base BC = 5 cm and ∠B=60∘.
View Solution