In the given figure, ABC is an equilateral triangle with co-ordinates of B and C as B(-3, 0) and C(3, 0). The co-ordinates of the vertex A are
To find the coordinates of vertex A of the equilateral triangle ABC, where B and C have coordinates B(-3, 0) and C(3, 0), we can follow these steps:
Step 1: Understand the properties of the triangle
Since ABC is an equilateral triangle, all sides are equal in length. The coordinates of points B and C are given, and we can determine the length of side BC.
Step 2: Calculate the length of side BC
The distance between points B and C can be calculated using the distance formula:
BC=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of B and C:
BC=√(3−(−3))2+(0−0)2=√(3+3)2=√62=6
Step 3: Determine the coordinates of point A
Since A is the vertex opposite side BC and lies on the y-axis, its x-coordinate is 0. Therefore, we can denote the coordinates of A as (0, y).
Step 4: Use the properties of the equilateral triangle
In an equilateral triangle, all sides are equal. Therefore, the lengths AB and AC must also be equal to 6. We will use the Pythagorean theorem to find the y-coordinate of point A.
Step 5: Apply the Pythagorean theorem
Using the Pythagorean theorem for triangle AOB (where O is the origin):
AB2=OA2+OB2
Here, AB=6 (length of side AB), OB=3 (the distance from the origin to point B), and OA=y (the distance from the origin to point A):
62=y2+32
36=y2+9
y2=36−9=27
y=√27=3√3
Step 6: Write the coordinates of point A
Thus, the coordinates of point A are:
A(0,3√3)
Final Answer:
The coordinates of vertex A are (0,3√3).
---
Since ABC is an equilateral triangle, all sides are equal in length. The coordinates of points B and C are given, and we can determine the length of side BC.
The distance between points B and C can be calculated using the distance formula:
BC=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of B and C:
BC=√(3−(−3))2+(0−0)2=√(3+3)2=√62=6
Since A is the vertex opposite side BC and lies on the y-axis, its x-coordinate is 0. Therefore, we can denote the coordinates of A as (0, y).
In an equilateral triangle, all sides are equal. Therefore, the lengths AB and AC must also be equal to 6. We will use the Pythagorean theorem to find the y-coordinate of point A.
Using the Pythagorean theorem for triangle AOB (where O is the origin):
AB2=OA2+OB2
Here, AB=6 (length of side AB), OB=3 (the distance from the origin to point B), and OA=y (the distance from the origin to point A):
62=y2+32
36=y2+9
y2=36−9=27
y=√27=3√3
Thus, the coordinates of point A are:
A(0,3√3)
The coordinates of vertex A are (0,3√3).
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Problems From NCERT/ Exemplar6videos
CO-ORDINATE GEOMETRY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Revision Exercise8videos
CO-ORDINATE GEOMETRY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE36videos
CONSTRUCTIONS
Similar Questions
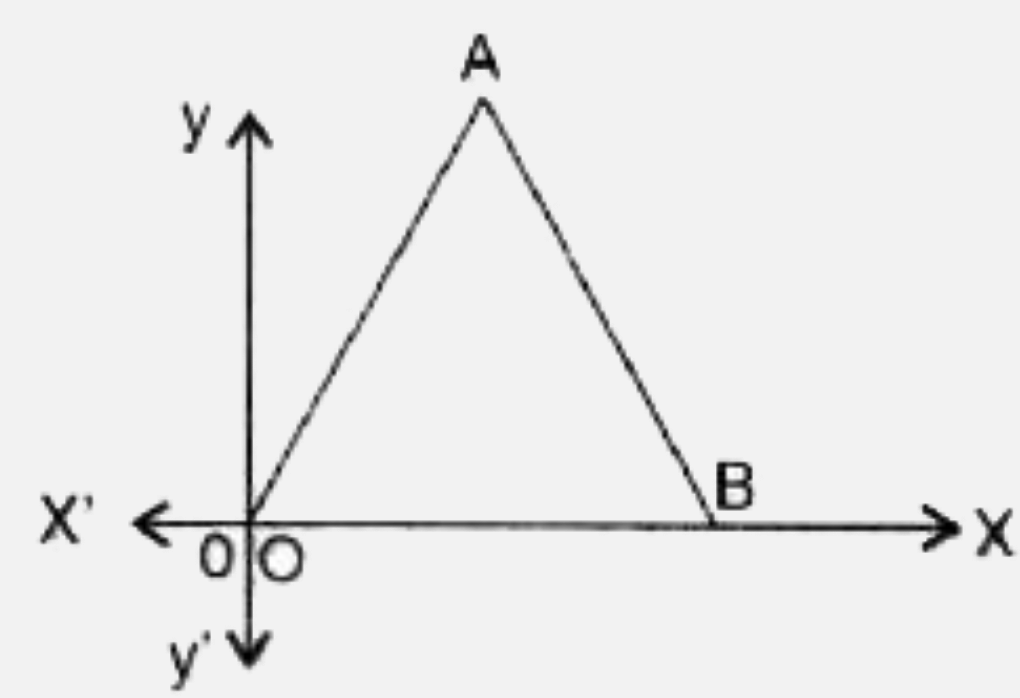
The given figure shows an equilateral triangle OAB.
If AB =2a units , find the co-ordinates of the vetices.
 View Solution
View SolutionThe slope of a median, drawn from the vertex A of the triangle ABC is -2. The co-ordinates of vertices B and C are respectively (-1, 3) and (3, 5). If the area of the triangle be 5 square units, then possible distance of vertex A from the origin is/are.
View SolutionThe base QR of an equilateral triangle PQR lies on X-axis. The co-ordinates of the point Q are (-4,0) and origin is the mid-point of the base. Find the co-ordinates of the points P and R.
View SolutionThe co-ordinates of three vertices of a parallelogram ABCD are A(1,0) , B(3,4) and C(1,2). The co-ordinates of fourth vertex D are :
View SolutionIf one vertex of an equilateral triangle of side 'a' lie at the origin and the other lies on the line x−√3y=0, the co-ordinates of the third vertex are:
View SolutionIn the following diagram, write down :

the co-ordinates of the points A, B and C.View SolutionFrom the given figure, find :
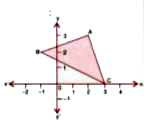
the co ordinates of A, B and C.View SolutionThree vertices of a parallelogram ABCD are B (6,7) , C (8,3) and D (0,−1) . Find the co-ordinates of vertex A .
View SolutionGiven a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
View SolutionIn ΔABC,∠A=90∘ and the co-ordinates of points B and C are (2,−4)and(1,5). Find the equation of the circumcircle of ΔABC.
View Solution

