The base QR of an equilateral triangle PQR lies on X-axis. The co-ordinates of the point Q are (-4,0) and origin is the mid-point of the base. Find the co-ordinates of the points P and R.
The correct Answer is:P(0,4√3)orP(0,−4√3)andR(4.0)
To solve the problem, we will follow these steps:
1. Identify the coordinates of points Q and R:
- Given that Q has coordinates (-4, 0) and the origin (0, 0) is the midpoint of the base QR, we can find the coordinates of R.
- Since the origin is the midpoint, the distance from Q to the origin is equal to the distance from the origin to R.
2. Calculate the coordinates of point R:
- The distance from Q (-4, 0) to the origin (0, 0) is 4 units.
- Therefore, point R must be 4 units to the right of the origin, which gives us the coordinates of R as (4, 0).
3. Determine the coordinates of point P:
- Since P is the apex of the equilateral triangle and lies above the x-axis, we denote its coordinates as (0, y).
- The lengths of the sides PQ, QR, and PR must all be equal.
4. Use the distance formula to find y:
- The distance PQ can be calculated as:
PQ=√(0−(−4))2+(y−0)2=√(4)2+y2=√16+y2
- The distance QR is:
QR=√(4−(−4))2+(0−0)2=√(8)2=8
- The distance PR can be calculated as:
PR=√(0−4)2+(y−0)2=√(−4)2+y2=√16+y2
5. Set the distances equal:
- Since PQ = QR, we have:
√16+y2=8
- Squaring both sides gives:
16+y2=64
- Rearranging gives:
y2=64−16=48
- Thus, y=±√48=±4√3.
6. Final coordinates of point P:
- Therefore, the coordinates of point P can be (0, 4√3) or (0, -4√3). Since P is above the x-axis, we take (0, 4√3).
Summary of Coordinates:
- Q = (-4, 0)
- R = (4, 0)
- P = (0, 4√3)
- Given that Q has coordinates (-4, 0) and the origin (0, 0) is the midpoint of the base QR, we can find the coordinates of R.
- Since the origin is the midpoint, the distance from Q to the origin is equal to the distance from the origin to R.
- The distance from Q (-4, 0) to the origin (0, 0) is 4 units.
- Therefore, point R must be 4 units to the right of the origin, which gives us the coordinates of R as (4, 0).
- Since P is the apex of the equilateral triangle and lies above the x-axis, we denote its coordinates as (0, y).
- The lengths of the sides PQ, QR, and PR must all be equal.
- The distance PQ can be calculated as:
PQ=√(0−(−4))2+(y−0)2=√(4)2+y2=√16+y2
- The distance QR is:
QR=√(4−(−4))2+(0−0)2=√(8)2=8
- The distance PR can be calculated as:
PR=√(0−4)2+(y−0)2=√(−4)2+y2=√16+y2
- Since PQ = QR, we have:
√16+y2=8
- Squaring both sides gives:
16+y2=64
- Rearranging gives:
y2=64−16=48
- Thus, y=±√48=±4√3.
- Therefore, the coordinates of point P can be (0, 4√3) or (0, -4√3). Since P is above the x-axis, we take (0, 4√3).
- Q = (-4, 0)
- R = (4, 0)
- P = (0, 4√3)
Topper's Solved these Questions
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Very Short Answer Questions
10 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
10 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Exercise 7c
14 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Long Answer Questions
2 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 11 B
10 Videos
Similar Questions
The co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively. Find :
the co-ordinates of the point where PQ intersects the x-axis.
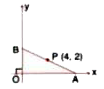
View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
View SolutionThe ordinate of a point lying on the line joining the points (6, 4) and (7, -5) is -23. Find the co-ordinates of that point.
View SolutionTwo uniform spheres A (Hollow) and B (solid) of same radius R (√125GmPr, where P is _____
View SolutionA point P lies on x-axis and another point Q lies on y-axis.
Write the ordinate of the point P.
View SolutionThe base of an equilateral triangle with side 20cm lies along x-axis such that the mid-point of the base is at the origin. Find the vertices of the triangle
View SolutionA point P lies on the x-axis and another point Q lies on the y-axis.
Write the ordinate of point P.
View SolutionThe point A(3, - 5) is reflected in the point P (-4, 3) as point A'. Find the co-ordinates of point A'.
View SolutionThe base of an equilateral triangle with side 2a lies along the y-axis such that the mid point of the base is at the origin. Find the vertices of the triangle.
View SolutionThe base of an equilateral triangle with side 2a lies along the y–axis such that the mid–point of the base is at the origin. Find vertices of the triangle.
View Solution
