Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
To find the coordinates of points A and D given that AB = BC = CD, with B = (0, 3) and C = (1, 8), we will follow these steps:
Step 1: Understand the relationship between the points
Since AB = BC = CD, points A, B, C, and D are evenly spaced along the line. This means that B is the midpoint between A and C, and C is the midpoint between B and D.
Step 2: Use the midpoint formula to find A
The midpoint formula states that if M is the midpoint of segment AB, then:
M=(x1+x22,y1+y22)
For points A (unknown coordinates (x, y)) and B (0, 3), and knowing that the midpoint M (which is point C) is (1, 8), we can set up the following equations:
1. For the x-coordinates:
x+02=1
2. For the y-coordinates:
y+32=8
Step 3: Solve for A's coordinates
1. From the x-coordinate equation:
x2=1⟹x=2
2. From the y-coordinate equation:
y+32=8⟹y+3=16⟹y=13
Thus, the coordinates of point A are (2, 13).
Step 4: Use the midpoint formula to find D
Now, we need to find the coordinates of point D. Since C is the midpoint between B and D, we can use the midpoint formula again:
For points B (0, 3) and D (unknown coordinates (x, y)), and knowing that the midpoint M (which is point C) is (1, 8), we can set up the following equations:
1. For the x-coordinates:
0+x2=1
2. For the y-coordinates:
3+y2=8
Step 5: Solve for D's coordinates
1. From the x-coordinate equation:
x2=1⟹x=2
2. From the y-coordinate equation:
3+y2=8⟹3+y=16⟹y=13
Thus, the coordinates of point D are (2, 13).
Final Answer
The coordinates of A are (-1, -2) and the coordinates of D are (2, 13).
Since AB = BC = CD, points A, B, C, and D are evenly spaced along the line. This means that B is the midpoint between A and C, and C is the midpoint between B and D.
The midpoint formula states that if M is the midpoint of segment AB, then:
M=(x1+x22,y1+y22)
For points A (unknown coordinates (x, y)) and B (0, 3), and knowing that the midpoint M (which is point C) is (1, 8), we can set up the following equations:
x+02=1
2. For the y-coordinates:
y+32=8
1. From the x-coordinate equation:
x2=1⟹x=2
2. From the y-coordinate equation:
y+32=8⟹y+3=16⟹y=13
Now, we need to find the coordinates of point D. Since C is the midpoint between B and D, we can use the midpoint formula again:
0+x2=1
2. For the y-coordinates:
3+y2=8
1. From the x-coordinate equation:
x2=1⟹x=2
2. From the y-coordinate equation:
3+y2=8⟹3+y=16⟹y=13
The coordinates of A are (-1, -2) and the coordinates of D are (2, 13).
Topper's Solved these Questions
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - EXERCISE 13 (C)
28 Videos
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - QUESTIONS
17 Videos
- SECTION AND MID-POINT FORMULABOOK - ICSECHAPTER - SECTION AND MID-POINT FORMULAEXERCISE - QUESTIONS
17 Videos
- SAMPLE PAPER 5 (MATHEMATICS)BOOK - ICSECHAPTER - SAMPLE PAPER 5 (MATHEMATICS)EXERCISE - SECTION C
8 Videos
- SHARES AND DIVIDENDSBOOK - ICSECHAPTER - SHARES AND DIVIDENDSEXERCISE - Exercise 3(C )
20 Videos
Similar Questions
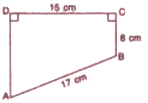
The given figure shows a trapezium ABCD in which AB = 17 cm, BC = 8 cm and CD = 15 cm. Find the area and perimeter of the trapezium.
View SolutionThree vertices of a parallelogram ABCD are B (6,7) , C (8,3) and D (0,−1) . Find the co-ordinates of vertex A .
View SolutionA park is in the shape of quadrilateral ABCD in which AB = 9 cm, BC = 12 cm, CD = 5 cm, AD = 8 cm and ∠C=90∘. Find the area of the park.
View SolutionThe three vertices of a parallelogram ABCD are A(-1,3,4), B(2,-1,3) and C(5,1,2). Find the co-ordinates of its 4th vertex D.
View SolutionA straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of points C and D.
View SolutionThe co-ordinates of the vertices of a parallelogram ABCD are A(-1,2,3), B(2, -4,1) and C(1,2,-1). Find the co-ordinates of its 4th vertex.
View SolutionThe co-ordinates of A, B, C are respectively (-4, 0), (0, 2) and (-3, 2). Find the co-ordinates of the point of intersection of the line which bisects the angle CAB internally and the line joining C to the middle point of AB is
View SolutionThe co-ordinates of two points A and B are (-3, 4) and (2, -1). Find :
the co-ordinates of the point where the line AB intersects the y-axis.
View SolutionABCD is a parallelogram where A(x,y),B(5,8),C(4,7)andD(2,−4). Find :
co-ordinates of A
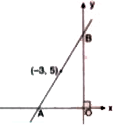
View SolutionThe mid - point of line segment AB (shown in the diagram) is (-3, 5), Find the co-ordinates of A and B.
 .
.
View Solution
