Find the area of the region bounded by y2=9x,x=2,x=4and the x-axis in the first quadrant.
Given curve y2=9x is a parabola which is symmetric to X-axis.
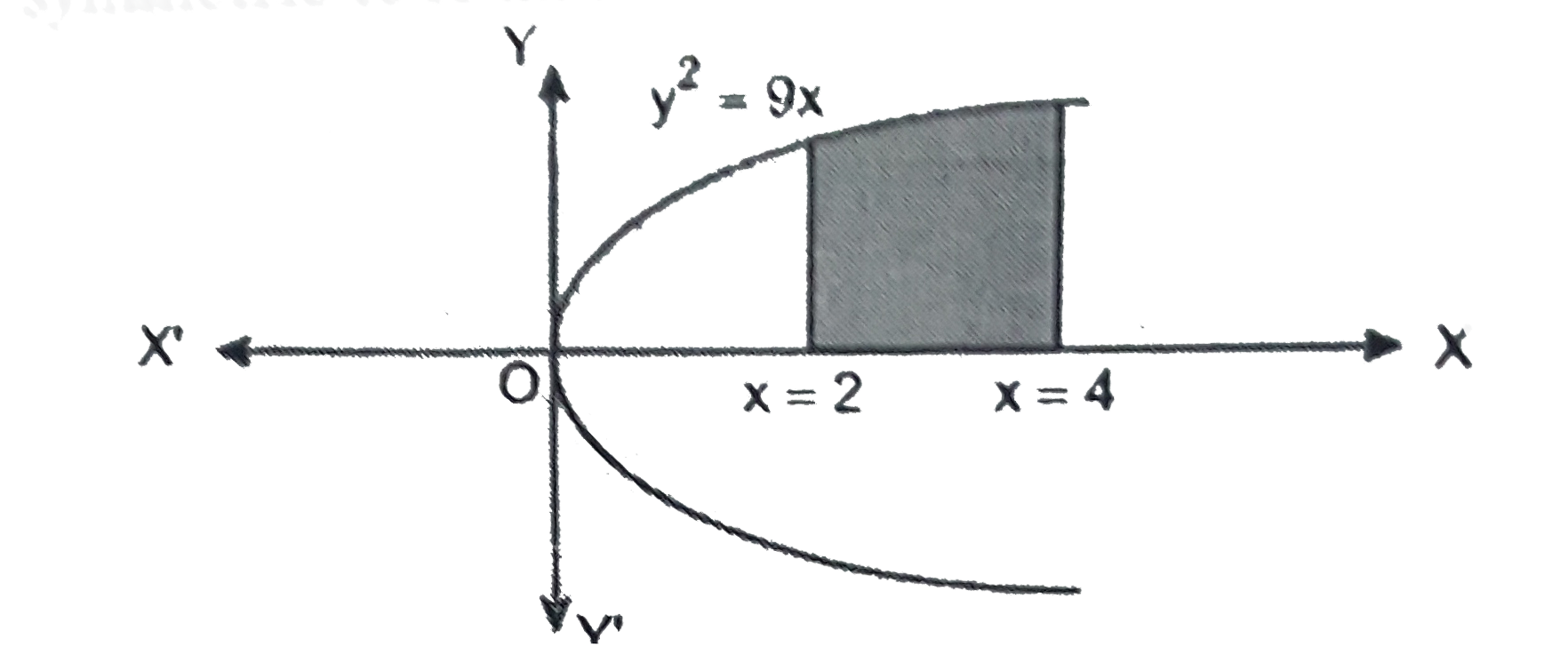
The area of the region bounded by the curve y2=9x,x=2 and x=4 and X-axis is shown in the figure.
∴ Required area
=∫42|y|dx=∫423√xdx
=3⎡⎣x3/232⎤⎦42=3×23(43/2−23/2)
=2(4√4−2√2)=2(8−2√2)
=4(4−√2) sq. units.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.27videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise19videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8 C Questions For Competitive Examinations10videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise24videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
Similar Questions
Find the area of the region bounded by x2=4y, y=2,y=4and the y-axis in the first quadrant.
View SolutionFind the area of the region bounded by x2=4y, y=2,y=4and the y-axis in the first quadrant.
View SolutionFind the area of the region bounded by y2=4x,x=1,x=4 and the x-axis in the first quadrant.
View SolutionFind the area of the region bounded by x2=16y, y=1, y=4 and the y-axis in the first quadrant.
View SolutionFind the area of the region bouonded by y2=4x,x=1,x=4 and x-axis in the first quadrant.
View SolutionFind the area of the region bounded by y =x2+1,y=x ,x=0 and y=2
View SolutionFind the area of the region bounded by
x2=8y, x-axis and the line x= 4View SolutionThe area of the region bounded by the curuse y=|x−2|,x=1,x=3 and the x-axis is
View SolutionThe area of the region bounded by the curves y=|x−2|,x=1,x=3 and the x-axis is
View SolutionFind the area of the region bounded by
y=cosx and the x axis in the interval [0,2π]View Solution

