The area between x=y2and x=4is divided into two equal parts by the linex=a, find the value of a.
The graph of y2=4ax is symmetric about X-axis which is shown below. x=a lies between the lines x=0 and x=4. According to the given condition.
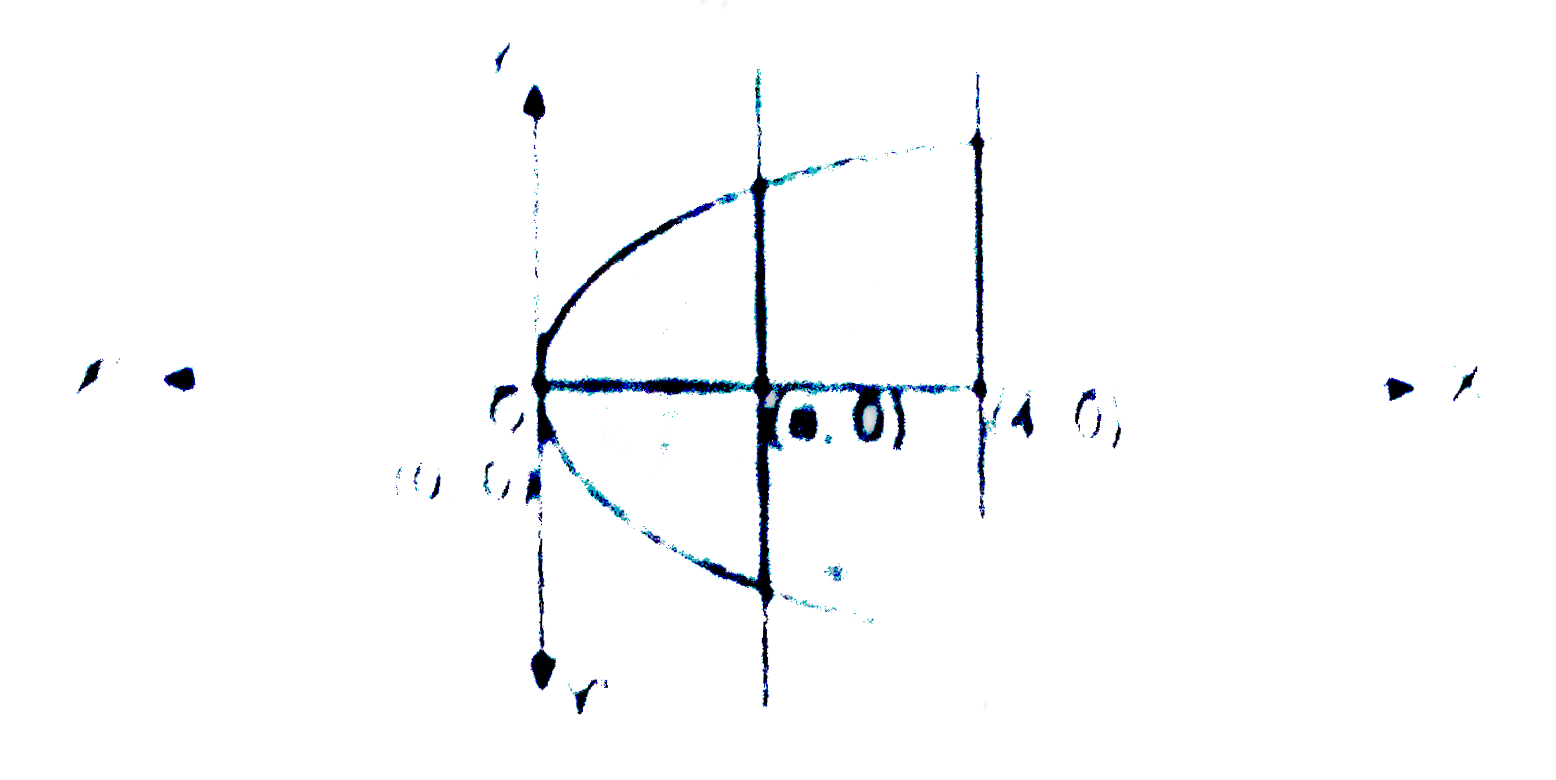
2∫a0ydx=2∫4aydx
⇒∫a02√a√xdx=∫4a2√a√xdx
⇒23[x3/2]a0=23[x3/2]4a
⇒a3/2=43/2−a3/2
⇒2a3/2=8⇒a3/2=4
⇒a=(4)2/3
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8.27videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise19videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Exercise 8 C Questions For Competitive Examinations10videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Miscellaneous Exercise24videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
Similar Questions
Area bounded by curve y2=x and x=4 is divided into 4 equal parts by the lines x=a and y=b then a&b is
View SolutionThe area bounded by the curve y=x2, the x-axis and the line x=213 is divided into two equal areas by the line x=k. The value of k is (A) 2−23 (B) 2−13 (C) 1 (D) 213−1
View SolutionThe circle x2+y2=4a2 is divided into two parts by the line x=3a2. Find the ratio of areas of these two parts.
View SolutionThe circle x2+y2=8 is divided into two parts by the parabola 2y=x2 . Find the area of both the parts.
View SolutionThe area enclosed by the circle x2+(y+2)2=16 is divided into two parts by the x-axis. Find by integration, the area of the smaller part.
View SolutionThe area between curve y=x2 and the line y=2 is
View SolutionTwo lines drawn through the point P (4, 0) divide the area bounded by the curve y=√2sin.πx4 and x-axis, between the lines x = 2 and x = 4, in to three equal parts. Sum of the slopes of the drawn lines is equal to:
View SolutionThe area between the curves y=x3 and y=x+|x| is equal to
View SolutionIf the point (a,a) is placed in between the lines |x+y|=4, then find the values of a.
View SolutionIf the point (a,a) is placed in between the lines |x+y|=4, then find the values of a.
View Solution

