In a circle of radius 7 cm, tangent PT is drawn from a point P such tht PT= 24 cm. If O is the centre of circle, then find the length of OP.
The correct Answer is:25cm
To find the length of OP in the given circle, we will use the Pythagorean theorem. Here’s the step-by-step solution:
Step 1: Understand the Geometry
We have a circle with center O and radius 7 cm. A tangent PT is drawn from point P outside the circle, and the length of the tangent PT is given as 24 cm. The radius OT is perpendicular to the tangent PT at point T.
Step 2: Identify the Right Triangle
Since OT is perpendicular to PT, we can form a right triangle OPT, where:
- OP is the hypotenuse,
- OT is one leg (the radius of the circle),
- PT is the other leg (the length of the tangent).
Step 3: Assign Known Values
From the problem:
- OT (radius) = 7 cm
- PT (tangent) = 24 cm
Step 4: Apply the Pythagorean Theorem
According to the Pythagorean theorem:
OP2=OT2+PT2
Step 5: Substitute the Known Values
Substituting the known values into the equation:
OP2=72+242
OP2=49+576
Step 6: Calculate the Sum
Now, calculate the sum:
OP2=625
Step 7: Find OP
To find OP, take the square root of both sides:
OP=√625
OP=25 cm
Conclusion
The length of OP is 25 cm.
---
We have a circle with center O and radius 7 cm. A tangent PT is drawn from point P outside the circle, and the length of the tangent PT is given as 24 cm. The radius OT is perpendicular to the tangent PT at point T.
Since OT is perpendicular to PT, we can form a right triangle OPT, where:
- OP is the hypotenuse,
- OT is one leg (the radius of the circle),
- PT is the other leg (the length of the tangent).
From the problem:
- OT (radius) = 7 cm
- PT (tangent) = 24 cm
According to the Pythagorean theorem:
OP2=OT2+PT2
Substituting the known values into the equation:
OP2=72+242
OP2=49+576
Now, calculate the sum:
OP2=625
To find OP, take the square root of both sides:
OP=√625
OP=25 cm
The length of OP is 25 cm.
Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Revision Exercise Short Answer Questions
4 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Revision Exercise Long Answer Questions
3 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise
32 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
10 Videos
Similar Questions
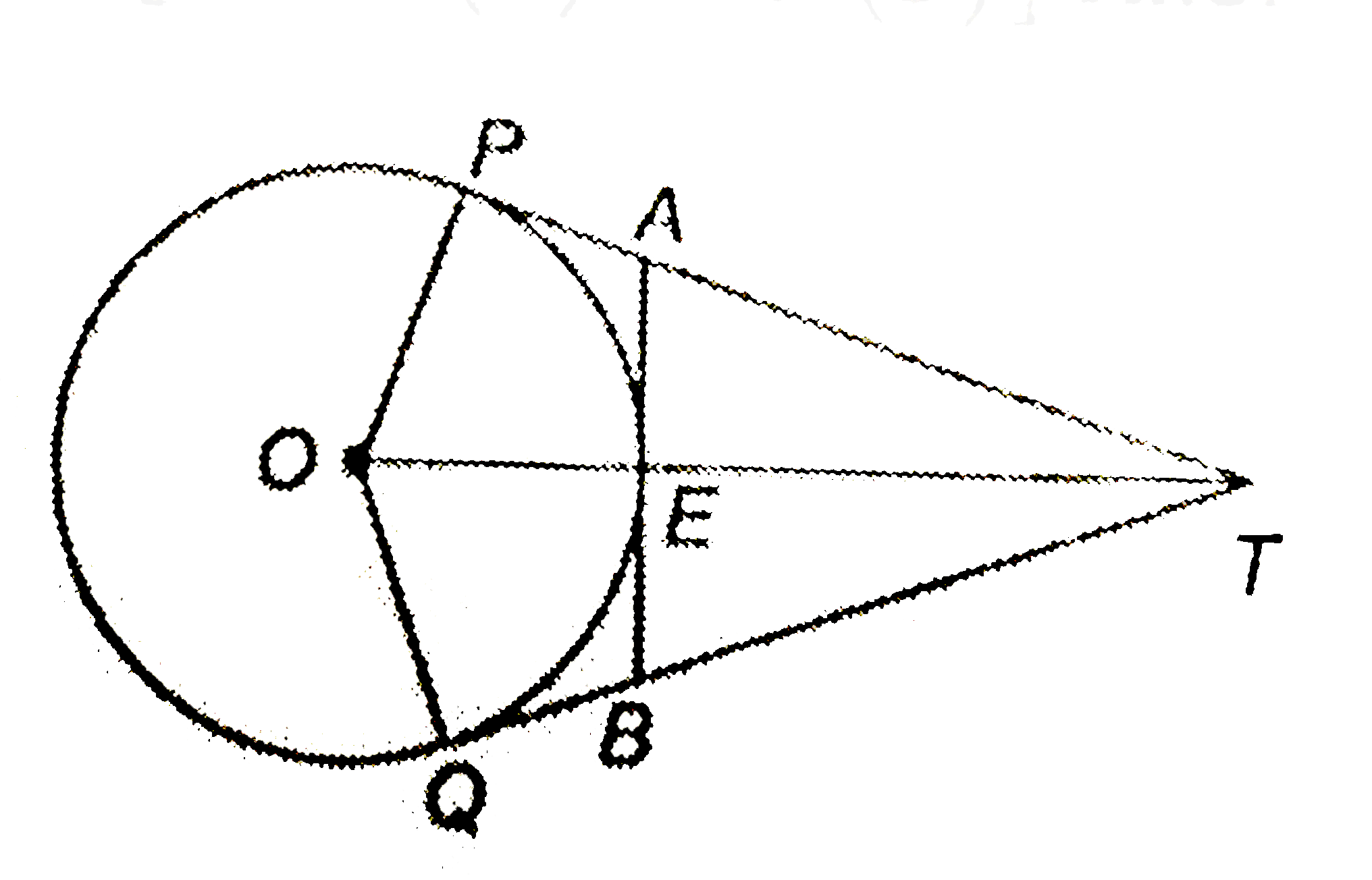
O is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
View SolutionAP is tangent to circle O at point P, What is the length of OP?
View SolutionIf the angle between two tangents drawn from an external point ‘P’ to a circle of radius ‘r’ and centre O is 60∘, then find the length of OP.
View SolutionIf the angle between two tangents drawn from an external point P to a circle of radius 'a' and centre O, is 60∘, then find the length of OP.
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
View SolutionType V: O is the center of the circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E . If AB is the tangent to the circle at E; find the length of AB.
View SolutionDraw a circle of radius 3 cm and take a point P outside it. Without using the centre of the circle draw two tangents of the circle from the point P.
View SolutionDraw a circle of radius 3 cm. Take a point P on it. Without using the centre of the circle, draw a tangent to the circle at point P.
View SolutionDraw a circle of radius 3 cm. Take a point P outside it. Without using the centre of the circle, draw two tangents to the circle from the point P.
View SolutionDraw a circle of radius 4 cm. Take a point P on it. Without using the centre of the circle, draw a tangent to the circle at point P .
View Solution
