The sides AB and DC of a cyclic quadrilateral ABCD when produced meet at E and the sides DA and CB when produced meet at F. Given ∠BEC=38∘,∠BAD=102∘. Find the values of ∠AFB and ∠ADC.
To solve the problem, we need to find the angles ∠AFB and ∠ADC in the cyclic quadrilateral ABCD given ∠BEC=38∘ and ∠BAD=102∘.
1. Identify the Angles in Triangle ADE:
- We know that ∠BEC=38∘ and ∠BAD=102∘.
- Let ∠AFB be x.
- In triangle ADE, the sum of the angles is 180∘.
- Therefore, we can write the equation:
x+102∘+38∘=180∘
2. Calculate x:
- Combine the known angles:
x+140∘=180∘
- Now, isolate x:
x=180∘−140∘=40∘
3. Find ∠ADC:
- Since ∠ADC is equal to x (which we found to be 40∘):
∠ADC=40∘
4. Find ∠AFB:
- In cyclic quadrilateral ABCD, the sum of opposite angles is 180∘.
- Let ∠ABC=y. Thus, we have:
y+102∘=180∘
- Solving for y:
y=180∘−102∘=78∘
5. Use Triangle FCD:
- In triangle FCD, we know ∠FCD=78∘ and ∠ADC=40∘.
- Let ∠AFB=z. Therefore:
z+78∘+40∘=180∘
- Combine the angles:
z+118∘=180∘
- Isolate z:
z=180∘−118∘=62∘
Final Answers:
- ∠AFB=62∘
- ∠ADC=40∘
- We know that ∠BEC=38∘ and ∠BAD=102∘.
- Let ∠AFB be x.
- In triangle ADE, the sum of the angles is 180∘.
- Therefore, we can write the equation:
x+102∘+38∘=180∘
- Combine the known angles:
x+140∘=180∘
- Now, isolate x:
x=180∘−140∘=40∘
- Since ∠ADC is equal to x (which we found to be 40∘):
∠ADC=40∘
- In cyclic quadrilateral ABCD, the sum of opposite angles is 180∘.
- Let ∠ABC=y. Thus, we have:
y+102∘=180∘
- Solving for y:
y=180∘−102∘=78∘
- In triangle FCD, we know ∠FCD=78∘ and ∠ADC=40∘.
- Let ∠AFB=z. Therefore:
z+78∘+40∘=180∘
- Combine the angles:
z+118∘=180∘
- Isolate z:
z=180∘−118∘=62∘
- ∠AFB=62∘
- ∠ADC=40∘
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
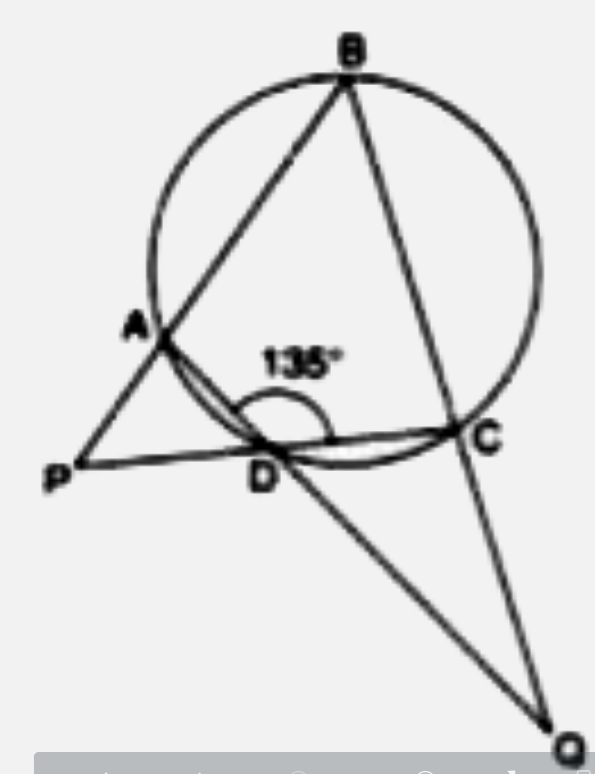
ABCD is a syclic quadrilateral with ∠ADC=135∘. Sides BA and CD produced meet at point P, sides AD and BC produced meet at point Q.If∠P:∠Q=2:1, find angles P and Q.
View SolutionABCD is a cyclic quadrilateral , Sides AB and DC produced meet at point E , whereas sides BC and AD produced meet at point F.
If ∠DCF:∠F:∠E=3:5:4 find the angles of the cyclic quadrilateral ABCD.
View SolutionIn a cyclic -quadrilateral PQRS angle PQR =135∘ , Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A:∠B=2:1. find angles A and B
View SolutionABCD is a cyclic quadrilateral in which AB and DC on being produced , meet at P such that PA = PD. Prove that AD is parallel to BC .
View SolutionIf one side of a cyclic quadrilateral is produced, then the exterior angle is equal to the interior opposite angle.
View SolutionIn the given figure,AB is parallel to DC. ∠BCE=80∘and∠BAC=25∘.F∈d:(i) angle CAD <br>(ii) angle CBD <br>(iii) angle ADC
View SolutionABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED=65∘ , Calculate
(i) ∠DAB
(ii) ∠BDC
View SolutionTwo alternate sides of a regular polygon, when produced, meet at right angle. Find:
the value of each exterior angle of the polygon.
View SolutionABCD is a cyclic quadrilateral in which BC is paralleld to AD, angle ADC=110∘ and angle BAC=50∘. Find angle DAC and angle DCA.
View SolutionIn the given figure ABCD is a cyclic quadrilateral in which AE is drawn parallel to CD and BA is produced. If ∠ABC=92∘ and ∠FAE=20∘, Find ∠BCD.

View Solution
