i) The radius of a circle is 40cm. Find the angle subtend by an arc of 22 cm at the center of circle in degrees.
To solve the problem of finding the angle subtended by an arc of 22 cm at the center of a circle with a radius of 40 cm, we can follow these steps:
1. Identify the Given Values:
- Radius of the circle (r) = 40 cm
- Length of the arc (L) = 22 cm
2. Use the Formula for Angle in Radians:
The angle (θ) subtended by an arc at the center of a circle can be calculated using the formula:
θ=Lr
where:
- θ is the angle in radians,
- L is the length of the arc,
- r is the radius of the circle.
3. Substitute the Values into the Formula:
θ=22 cm40 cm=2240=1120 radians
4. Convert Radians to Degrees:
To convert radians to degrees, use the conversion factor:
Degrees=θ×180π
Substitute θ:
Degrees=1120×180π
5. Simplify the Expression:
Degrees=11×18020×π=198020π=99π degrees
6. Calculate the Approximate Value:
Using the value of π (approximately 3.14):
99π≈993.14≈31.62 degrees
Final Answer:
The angle subtended by the arc of 22 cm at the center of the circle is approximately 31.62 degrees.
---
- Radius of the circle (r) = 40 cm
- Length of the arc (L) = 22 cm
The angle (θ) subtended by an arc at the center of a circle can be calculated using the formula:
θ=Lr
where:
- θ is the angle in radians,
- L is the length of the arc,
- r is the radius of the circle.
θ=22 cm40 cm=2240=1120 radians
To convert radians to degrees, use the conversion factor:
Degrees=θ×180π
Substitute θ:
Degrees=1120×180π
Degrees=11×18020×π=198020π=99π degrees
Using the value of π (approximately 3.14):
99π≈993.14≈31.62 degrees
The angle subtended by the arc of 22 cm at the center of the circle is approximately 31.62 degrees.
Topper's Solved these Questions
- TRIGNOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - EXERCISES 3B
24 Videos
- TRIGNOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - EXERCISES 3C
18 Videos
- TRIGNOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE
10 Videos
- STRAIGHT LINESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise
207 Videos
Similar Questions
Knowledge Check
The angle subtended by an arc of length 20 cm at the centre of circle when radius is 14 cm is
A57 radiansB107 radiansC514 radiansD710 radians
The radius of a circle is 3.6 cm. Find the length of the arc of the sector with central angle 36∘
View SolutionThe radius of a circle is given as 15 cm and chord AB subtends an angle of 131∘ at the centre C of the circle . Using trigonometry. calculate :
the length of AB,
View SolutionA circular arc of length π cm. Find angle subtended by it at the centre in radian and degree.
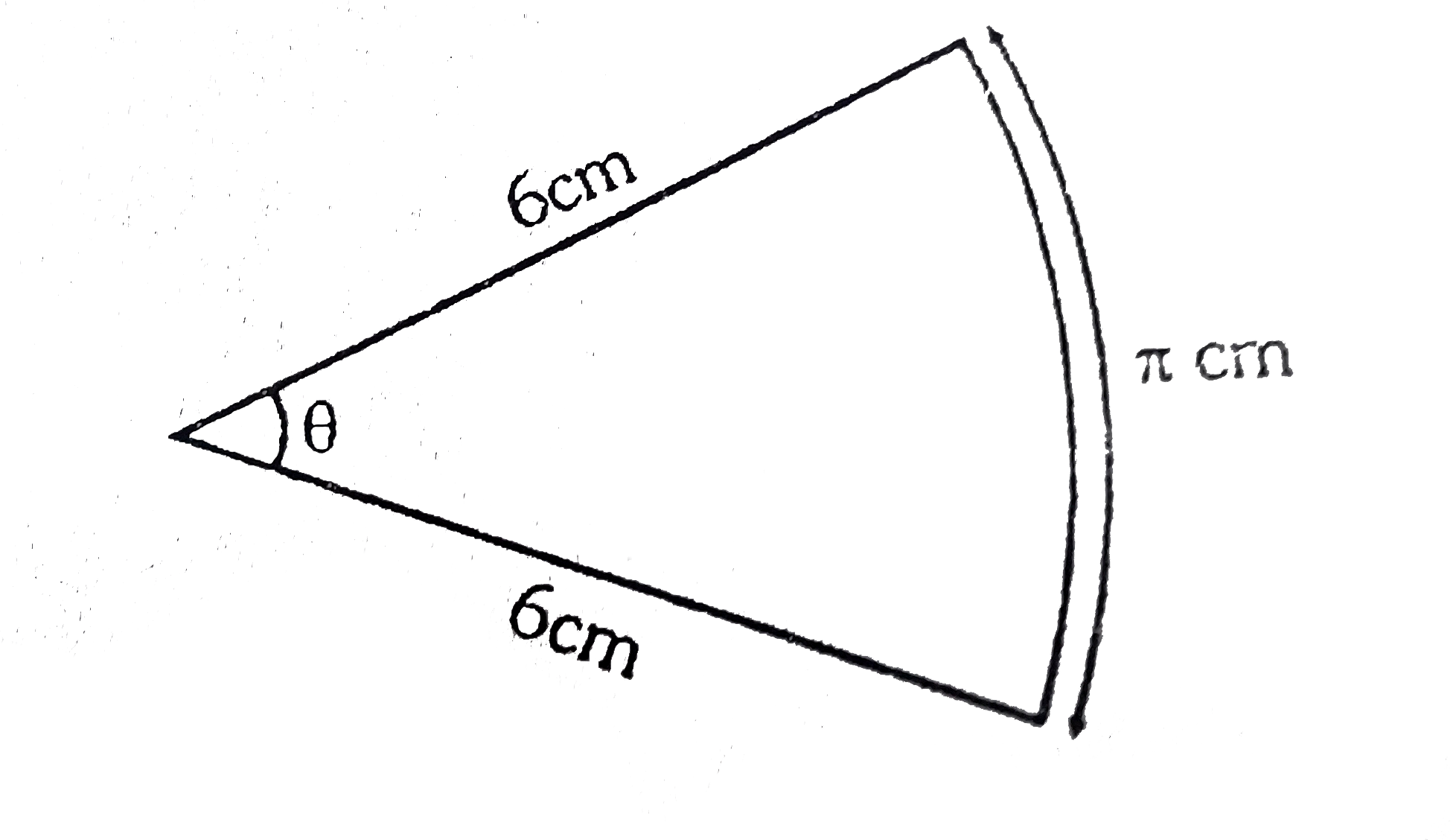
View SolutionThe chord of a circle is equal to its radius, find the angle subtended by this chord at the centre.
View SolutionThe radius of a circle is 30 cm. find the length of an arc this circle, if the length of the chord of the arc is 30 cm.
View SolutionThe radius of a circle is 30 cm. find the length of an arc this circle, if the length of the chord of the arc is 30 cm.
View SolutionFind the radius of a circle in which an arc of 37.4 cm subtends an angle of 60∘ at the center.
View Solution