CE and DE are equal chords of a cricule with centre O. if ∠AOB=90∘find ar(△CED):ar(△AOB)
To find the ratio of the areas of triangles CED and AOB, we can follow these steps:
1. Understanding the Given Information:
- We have a circle with center O.
- CE and DE are equal chords, which means CE = DE.
- Angle AOB = 90°.
2. Identifying Properties of the Triangles:
- Since CE = DE, triangle CED is isosceles.
- In triangle AOB, angle AOB is given as 90°, making it a right triangle.
3. Finding Angles in Triangle CED:
- Let the angles at C and D be equal (let's call them angle 1 and angle 2).
- Since triangle CED is isosceles, angle 1 = angle 2.
- The sum of angles in triangle CED is 180°.
- Therefore, angle 1 + angle 2 + angle CED = 180°.
- Since angle 1 = angle 2, we can write: 2 * angle 1 + angle CED = 180°.
- We know that angle CED is subtended by the diameter (since CE and DE are chords), which means angle CED = 90°.
- Thus, 2 * angle 1 + 90° = 180°.
- This gives us 2 * angle 1 = 90°, leading to angle 1 = 45°.
4. Finding Angles in Triangle AOB:
- In triangle AOB, we already have angle AOB = 90°.
- Since OA = OB (both are radii of the circle), triangle AOB is also isosceles.
- Therefore, angle OAB = angle OBA.
- Let angle OAB = angle OBA = angle 3.
- The sum of angles in triangle AOB gives us: angle 3 + angle 3 + 90° = 180°.
- This leads to 2 * angle 3 + 90° = 180°.
- Thus, 2 * angle 3 = 90°, giving us angle 3 = 45°.
5. Establishing Similarity:
- Now we have angle CED = 90°, angle C = 45°, and angle D = 45° in triangle CED.
- In triangle AOB, angle AOB = 90°, angle OAB = 45°, and angle OBA = 45°.
- Since both triangles have the same angles, triangle CED is similar to triangle AOB.
6. Finding the Ratio of Areas:
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
- Let the length of the chord CE (or DE) be CD = 2R (where R is the radius of the circle).
- The hypotenuse AB in triangle AOB can be calculated using the Pythagorean theorem:
- AB² = OA² + OB² = R² + R² = 2R².
- Therefore, AB = R√2.
- Now, the ratio of the sides (CD to AB) is:
- CD / AB = (2R) / (R√2) = 2 / √2 = √2.
- Therefore, the ratio of the areas is:
- Area of triangle CED / Area of triangle AOB = (CD / AB)² = (√2)² = 2.
Final Answer:
The ratio of the areas of triangle CED to triangle AOB is 2:1.
- We have a circle with center O.
- CE and DE are equal chords, which means CE = DE.
- Angle AOB = 90°.
- Since CE = DE, triangle CED is isosceles.
- In triangle AOB, angle AOB is given as 90°, making it a right triangle.
- Let the angles at C and D be equal (let's call them angle 1 and angle 2).
- Since triangle CED is isosceles, angle 1 = angle 2.
- The sum of angles in triangle CED is 180°.
- Therefore, angle 1 + angle 2 + angle CED = 180°.
- Since angle 1 = angle 2, we can write: 2 * angle 1 + angle CED = 180°.
- We know that angle CED is subtended by the diameter (since CE and DE are chords), which means angle CED = 90°.
- Thus, 2 * angle 1 + 90° = 180°.
- This gives us 2 * angle 1 = 90°, leading to angle 1 = 45°.
- In triangle AOB, we already have angle AOB = 90°.
- Since OA = OB (both are radii of the circle), triangle AOB is also isosceles.
- Therefore, angle OAB = angle OBA.
- Let angle OAB = angle OBA = angle 3.
- The sum of angles in triangle AOB gives us: angle 3 + angle 3 + 90° = 180°.
- This leads to 2 * angle 3 + 90° = 180°.
- Thus, 2 * angle 3 = 90°, giving us angle 3 = 45°.
- Now we have angle CED = 90°, angle C = 45°, and angle D = 45° in triangle CED.
- In triangle AOB, angle AOB = 90°, angle OAB = 45°, and angle OBA = 45°.
- Since both triangles have the same angles, triangle CED is similar to triangle AOB.
- The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
- Let the length of the chord CE (or DE) be CD = 2R (where R is the radius of the circle).
- The hypotenuse AB in triangle AOB can be calculated using the Pythagorean theorem:
- AB² = OA² + OB² = R² + R² = 2R².
- Therefore, AB = R√2.
- Now, the ratio of the sides (CD to AB) is:
- CD / AB = (2R) / (R√2) = 2 / √2 = √2.
- Therefore, the ratio of the areas is:
- Area of triangle CED / Area of triangle AOB = (CD / AB)² = (√2)² = 2.
The ratio of the areas of triangle CED to triangle AOB is 2:1.
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
AB and CD are two equal chords of a circle with centre O which intersect each other at right angle at point P. If OM ⊥ AB and ON ⊥ CD, show that OMPN is a square.
View SolutionAB and CD are two equal chords of a circle with centre O which intersect each other at right angle at P. If OM ⊥ AB and ON ⊥ CD, show that OMPN is a square.
View SolutionIn the adjoining figure, ∠ADB and ∠ACB are the angles in the same segment and chord AC passes through the centre O. If ∠CAB=40∘ then find the value of ∠ADB.

View SolutionIf AB, BC and CD are equal chords of a circle with O as centre and AD diameter, then ∠AOB= (a) 600 (b) 900 (c) 1200 (d) none of these
View SolutionIn the adjoining figure, DE is a chord parallel to diameter AC to the circle with centre. O if ∠CBD=60∘. Calculate ∠CDE.

View SolutionIn the given figure, AB and CD are two equal chords of a circle, with centre O. If P is the mid-point of chord AB, Q is the mid-point of chord CD and ∠POQ=150∘ find angleAPQ
View SolutionIn AB, DE and GF are parallel to each other and AD, BG and EF ar parallel to each other . If CD: CE = CG:CB = 2:1 then the value of area (△AEG):area(△ABD) is equal to (a) 7/2 (b)3 (c)4 (d)9/2
View SolutionIn circle given below . O is its centre and lengths of chords AB and CD are in the ratio 5 :3
If angle AOB = 100∘, find :
(i)∠COD

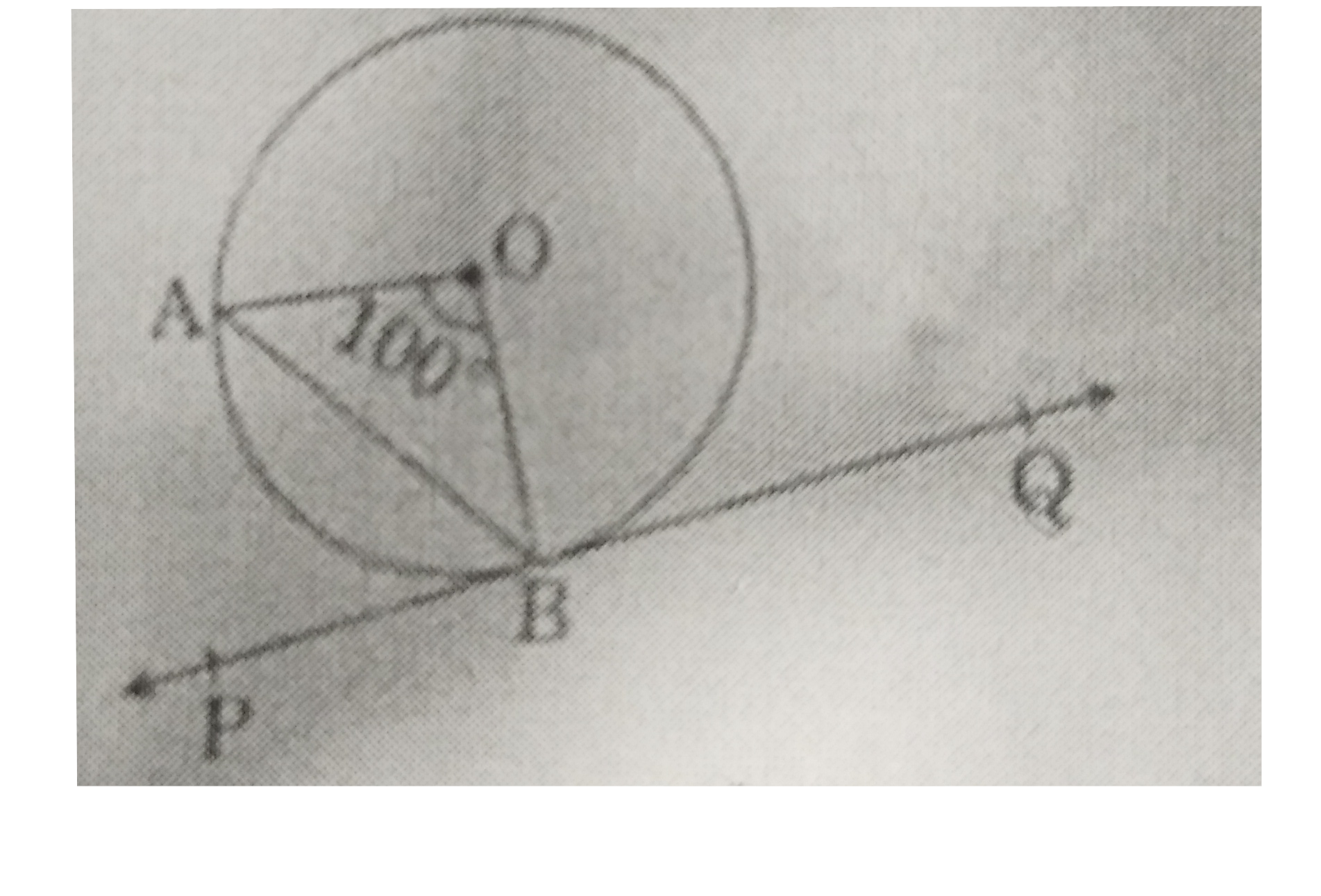
View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
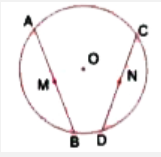
∠AMN=∠CNM.
View Solution
