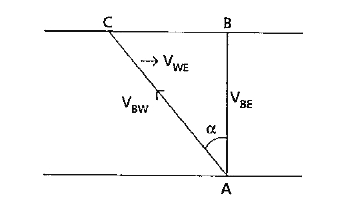
Show that a boat must move at an angle with respect to river water in order to cross the river in minimum time.
If the boat has to move along the line AB, the resultant velocity of VBE should be directed along AB and the boat reaches the point B directly. For this to happen the boat velocity with respect to water VBW should be directed such that it makes an angle α with the line AB upstream as shown in the figure.
VWEVBW=sinα⇒α=sin−1(VWEVBW)
and VBE=√V2BW−V2WE
The minimum time taken by the boat to cross the river
t=ABVBE
t=AB√V2BW−V2WE
Similar Questions
Crossing River In Minimum Time
View SolutionA boat can be rowed at 5 m/s on still water. It is used to cross a 200m wide river from the south bank to the north bank. The river current has uniform velocity of 3 m/s due east.
(a) In which direction must it be steered to cross the river perpendicular to current ?
(b) How long will it take to cross the river in a direction perpendicular to the river flow ?
(c) In which direction must the boat be steered to cross the river in minimum time ? How far will it drift ?
View Solution
Knowledge Check
A boat crossing a river moves with a velocity v relative to still water. The river is flowing with a velocity v/2 with respect to the bank. The angle with respect to the flow direction with which the boat should move to minimize the drift is–
A30∘B60∘C150∘D120∘STATEMENT-1: A man can cross river of width d in minimum time t. On increasing river velocity, minimum time to cross the river by man will remain uncharged.
STATEMENT-2: Velocity of river is perpendicular to width of river. So time to cross the river is independent of velcoity of river.AStatement-I is true, Statement-II is true, Statement-II is correct explanation for Statement-IBStatement-I is true, Statement-II is true, Statement-II is NOT a correct explanation for Statement-ICStatement-I is true, Statement-II is falseDStatement-I is false, Statement-II is true.
A boat can be rowed at 5 m/s on still water. It is used to cross a 200m wide river from the south bank to the north bank. The river current has uniform velocity of 3 m/s due east.
(a) In which direction must it be steered to cross the river perpendicular to current ?
(b) How long will it take to cross the river in a direction perpendicular to the river flow ?
(c) In which direction must the boat be steered to cross the river in minimum time ? How far will it drift ?
View SolutionA boat is moving with a velocity (3ˆi+ˆj) with respect to ground. The water in the river is moving with a velocity −3ˆi−4ˆj with respect to ground. What is the relative velocity of boat with respect to river ?
View SolutionA rever 500m wide flows at a rate at a rate of 4kmh−1. A swinmmer who can swin at 8kmh−1. In still water, wishes to cross the river straight . (i) Along what direection must he strike? (ii) What should be his resultant velocity. (ii) What is the time of crossing the river?
View SolutionThe river 500 m wide is flowing with a current of 4kph. A boat starts from one bank of the river wishes to cross the river at right angle to stream direction. Boatman can row the boat at 8 kph. In which direction he should row the boat. What time he ''ll take to cross the river ?
View SolutionA man wishes to cross a river which is flowing at a certain speed . Man uses a motor boat whose velocity with respect to water is more than speed of flow. Minimum possible time the boat takes to cross the river is t1 , but drift along the length of river is x . When boat takes shortest route to cross the river , then it takes time t2 . Find the velocity of boat with respect to water .
View SolutionSTATEMENT-1: A man can cross river of width d in minimum time t. On increasing river velocity, minimum time to cross the river by man will remain unchanged.
STATEMENT-2: Velocity of river is perpendicular to width of river. So time to cross the river is independent of velcoity of river.
View Solution
