A stone of mass m tied to the end of a string revolves in a vertical circle of radius R . The net forces at the lowest and highest points of the circle directed vertically downwards are : ( Choose the correct alternative )
Lowest PointHighest Point(a)mg−T1mg+T2(b)mg+T1mg−T2(c)mg+T1−(mv21)Rmg−T2+(mv21)R(d)mg−T1−(mv21)/Rmg+T2+(mv21)/R
T1andv1 denote the tension and speed at the lowest point T2andv2 denote corresponding values at the highest point .
The net force at lowest point α is FL=(mg1−T1) and the net force at the highest point H is FH=mg+T2 .
Similar Questions
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative]

T1 and V1 denote the tension and speed at the lowest point T2 and V2 denote the corresponding values at the highest points.
View SolutionA stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative] Lowest point Highest point
T1 and V1 denote the tension and speed at the lowest point T2 and V2 denote the corresponding values at the highest points.
View Solution
Knowledge Check
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative] Lowest point Highest point
T1 and V1 denote the tension and speed at the lowest point T2 and V2 denote the corresponding values at the highest points.Amg−T1mg+T2Bmg+T1mg−T2Cmg+T1−(mv21)/Rmg−T+(mv21)/RDmg−T1−(mv21)/Rmg+t2+(mv21)/RA main revolves a stone of mass m tied to the end of a string in a circle of radius R The net force at the lowest and height point of the circle directed vertical downward are
Here T1,T2 and (v1,v2) denote the tension in the string (and the speed of the stone) at the lowest and highest points, respectively.ALowest pointhighest pointmg−T1mg+T2BLowest pointhighest pointmg+T1mg−T2CLowest pointhighest pointmg+T1−mv2rmg−T2+mv2rDLowest pointhighest pointmg−T1−m1v21Rmg+T+m1v21RA particle A of mass m is attached to a vertical axis by two stings PA and QA of lengths 3L and 4L , respectively. PQ=5L. A rotates around the axis with an angular speed ω. The tension in the two strings are T1 and T2.
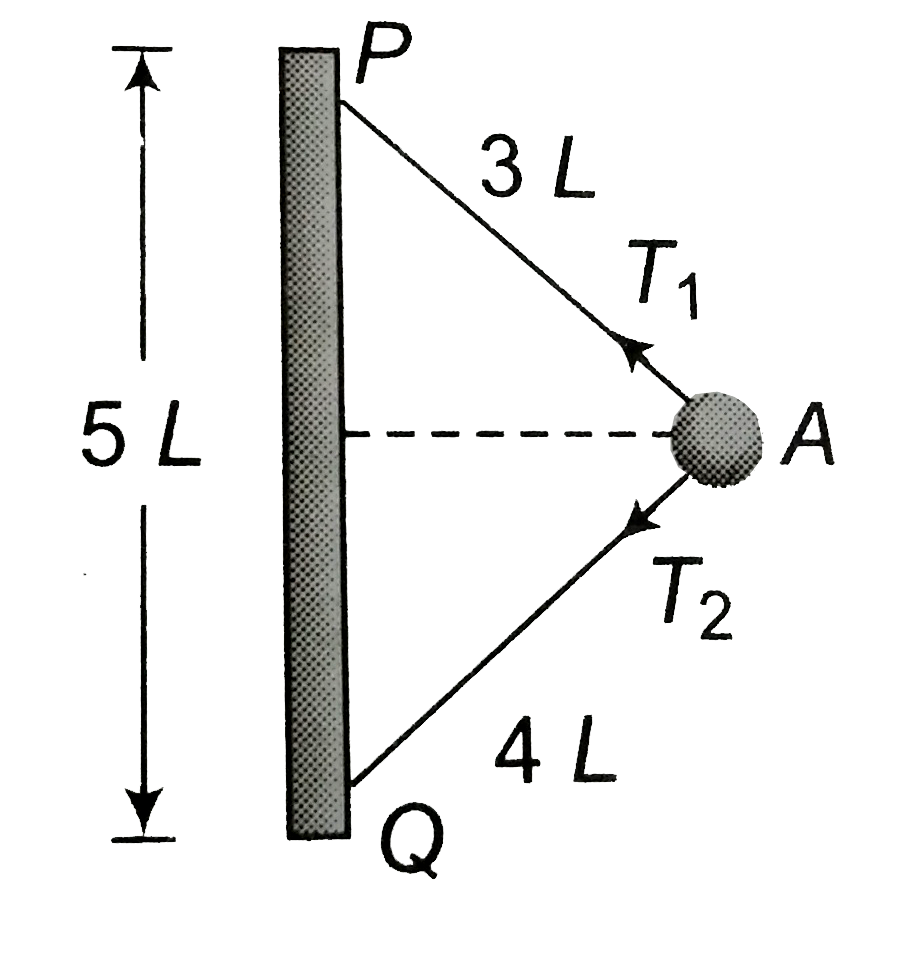
(i) T1=T2
(ii) 3T1−4T2=5mg
(iii) 4T1+3T2=12mω2LA(i)onlyB(i),(ii)C(i),(iii)D(ii),(iii)
A small body of mass m is tried to a string and revolved in a vertical circle of radius r. If the tension in the string at the highest point is mg, what is its speed there?
View SolutionA stone of mass m tied to one end of a string is revolved in a vertical circle of radius R the net forces at the lowest (FL and highest (FH) points of the circle directed vertically downwards are :
(a) FL=mg−T1FH=mg+T2
(b) FL=mg+T1,FH=mg−T2
(c) FL=mg+T1−mυ21R,FH=mg−T2+mυ21R
(d) FL=mg−T1−mυ21R,FH=mg+T2+mυ12R
Choose corret alternative T1,υ1 denote the tension and speed at the lowest point T2,υ2 denote corresponding valuse at the highest point .
View SolutionIf t1 and t2 are the lengths of tangents drawn on circle with radius r from two conjugate points A,B then t21+t22=
View SolutionA particle of mass m is suspended from a string so that it can move in a circular path in vertical plane. It is given v=3√glat the bottom most point. Match the values of tension in string at A,B,C,D

Column IColumn II(A) TA(P) 10 mg ),((B) T_(B),,(Q)7mg),((C) T_(C),,(R)4mg),((D) T_(D),,(S)5mg),(,,(T)5.5mg
View SolutionThe normal drawn at a point (at12,−2at1) of the parabola y2=4ax meets it again in the point (at22,2at2), then t2=t1+2t1 (b) t2=t1−2t1 t2=−t1+2t1 (d) t2=−t1−2t1
View Solution
