Two particles of mass m and 2m have their position vectors as a function of time as $r_{1} (t) = t ˆ i + t^{3} ˆ j + 2 t^{2} ˆ k and r_{1} (t) = t ˆ i + t^{3} ˆ j + t^{2} ˆ k$ respectively (where t is the time). Which one of the following graphs represents the path of the centre of mass?

A

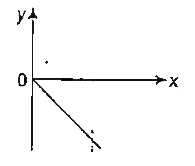
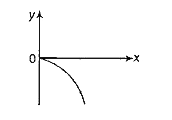
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Text Solution

Verified by Experts

The correct Answer is:D

Path of the centre of mass in a two particle system, $r (t) = [\frac{m_{1} r_{1} (t) + m_{2} r_{2} (t)}{m_{1} + m_{2}}] or r (t) = ⎡ ⎢ ⎢ ⎣ \frac{m t ˆ i - t^{3} ˆ j + 2 t^{2} ˆ k + 2 m (t ˆ i - t^{3} ˆ j - t^{2} ˆ k)}{m + 2 m} ⎤ ⎥ ⎥ ⎦$
$\Rightarrow r (t) = \frac{3 t ˆ i - 3 t^{3} ˆ j}{3} = t ˆ i - t^{3} ˆ j$
According above result option (d ) is correct

|

Updated on:21/07/2023

Class 12 PHYSICS SOLVED PAPER 2018

Similar Questions

Knowledge Check

Question 1 - Select One
The position vectors of three particles of mass $m_{1} = 1 k g, m_{2} = 2 k g and m_{3} = 3 k g$ are $r_{1} = (ˆ i + 4 ˆ j + ˆ k)$ m, $r_{2} = (ˆ i + ˆ j + ˆ k)$ m and $r_{3} = (2 ˆ i - ˆ j - ˆ 2 k)$ m, respectively. Find the position vector of their center of mass.
A $r_{c m} = \frac{1}{2} (3 i + j - 2 k) m$
B $r_{c m} = \frac{1}{2} (3 i + 2 j - k) m$
C $r_{c m} = \frac{1}{2} (3 i + 3 j - k) m$
D $r_{c m} = \frac{1}{2} (3 i + j - k) m$
Question 2 - Select One
Find the area of triangle if position vector of vertices w.r.t. O is $- ˆ i + 2 ˆ j + 3 ˆ k, 2 ˆ i - ˆ j - ˆ k, ˆ i + ˆ j - ˆ k .$
A $\frac{\sqrt{89}}{2} s q . u n i t s$
B $\frac{89}{2} s q . u n i t s$
C $\frac{2}{\sqrt{79}} s q . u n i t s$
D $\frac{79}{2} s q . u n i t s$

Recommended Questions

Home
Ask Doubt
Profile