Four resistances each of 1Ω are connected to form a square. Find the resistance across any one side of the square.
Let us find the net resistance between B and C
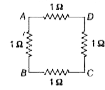
Here, RBA,RADandRDC are in series.
So, Rs=1+1+1=3Ω
Since, Rs is in parallel with RBC.
So, Req=RP=RsRBCRs+RBC=3×13+1=34=0.75Ω
Similar Questions
Knowledge Check
Three resistance each of 4Ω are connected to form a triangle. The resistance between any two terminals is
A12ΩB2ΩC6ΩD83ΩFour resistances of 100Ω each are connected in the form of square. Then, the effective resistance along the diagonal points is
A200ΩB400ΩC100ΩD150ΩIf Four resistors each of 1Ω are connected in parallel the effective resistances will be
A0.5ΩB0.25ΩC4ΩD2Ω
Four resistances, each of 10Ω, are connected to form a square as shown in (Fig. 3.52), find the equivalent resistance between the opposite corners AandC.
 .
.
View SolutionA 16Ω wire is bend to form a square loop. A 9 V supply having internal resistance of 1Ω is connected across one of its sides. The potential drop across the diagonals of the square loop is _______×10−1V
View SolutionFour resistances of 2.0 Ω each are joined end to end, to form a square ABCD. Calculate the equivalent resistance of the combination between any two adjacent corners
View SolutionFour resistances 10, 10 , 10 and 15Ω are connected so as to form Wheatstone's bridge. The resistance connected across 15Ω resistance to balance the bridge is
View SolutionSix equal resistances, each 1Ω, are joined to form a network as showing figure Then the resistance between any two corners is
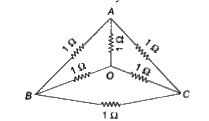
View Solution

 .
.