Three resistance each of 4Ω are connected to form a triangle. The resistance between any two terminals is
12Ω
2Ω
6Ω
83Ω
The correct Answer is:D
To find the equivalent resistance between any two terminals of a triangle formed by three resistances of 4 ohms each, we can follow these steps:
1. Identify the Configuration:
We have three resistors, each of 4 ohms, connected in a triangular configuration. Let's label the vertices of the triangle as A, B, and C.
2. Visualize the Circuit:
The resistances can be represented as follows:
- Resistance R1 (between A and B) = 4 ohms
- Resistance R2 (between B and C) = 4 ohms
- Resistance R3 (between C and A) = 4 ohms
3. Choose Two Terminals:
We will find the equivalent resistance between terminals A and B.
4. Analyze the Circuit:
When a current enters terminal A, it can either go directly to terminal B through R1 or go to terminal C through R3 and then to terminal B through R2.
5. Combine Resistors:
The resistors R2 and R3 are in series when considering the path from A to B through C. Therefore, their equivalent resistance (R23) is:
R23=R2+R3=4Ω+4Ω=8Ω
6. Combine with R1:
Now, the equivalent resistance R23 (8 ohms) is in parallel with R1 (4 ohms). The formula for the equivalent resistance (R_eq) of two resistors in parallel (R1 and R23) is given by:
1Req=1R1+1R23
Substituting the values:
1Req=14+18
To combine these fractions, we find a common denominator (8):
1Req=28+18=38
7. Calculate R_eq:
Taking the reciprocal gives us:
Req=83Ω
Final Answer:
The equivalent resistance between any two terminals (A and B) is:
Req=83Ω
We have three resistors, each of 4 ohms, connected in a triangular configuration. Let's label the vertices of the triangle as A, B, and C.
The resistances can be represented as follows:
- Resistance R1 (between A and B) = 4 ohms
- Resistance R2 (between B and C) = 4 ohms
- Resistance R3 (between C and A) = 4 ohms
We will find the equivalent resistance between terminals A and B.
When a current enters terminal A, it can either go directly to terminal B through R1 or go to terminal C through R3 and then to terminal B through R2.
The resistors R2 and R3 are in series when considering the path from A to B through C. Therefore, their equivalent resistance (R23) is:
R23=R2+R3=4Ω+4Ω=8Ω
Now, the equivalent resistance R23 (8 ohms) is in parallel with R1 (4 ohms). The formula for the equivalent resistance (R_eq) of two resistors in parallel (R1 and R23) is given by:
1Req=1R1+1R23
Substituting the values:
1Req=14+18
To combine these fractions, we find a common denominator (8):
1Req=28+18=38
Taking the reciprocal gives us:
Req=83Ω
The equivalent resistance between any two terminals (A and B) is:
Req=83Ω
Similar Questions
Three resistors each of 2 ohm are connected together in a triangular shape. The resistance between any two vertices will be
View SolutionA uniform metallic wire has a resistance of 18 Ω and is bent into an equiolateral triangle. Then, the resistance between any two vertices of the triangle is :
View SolutionFive resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
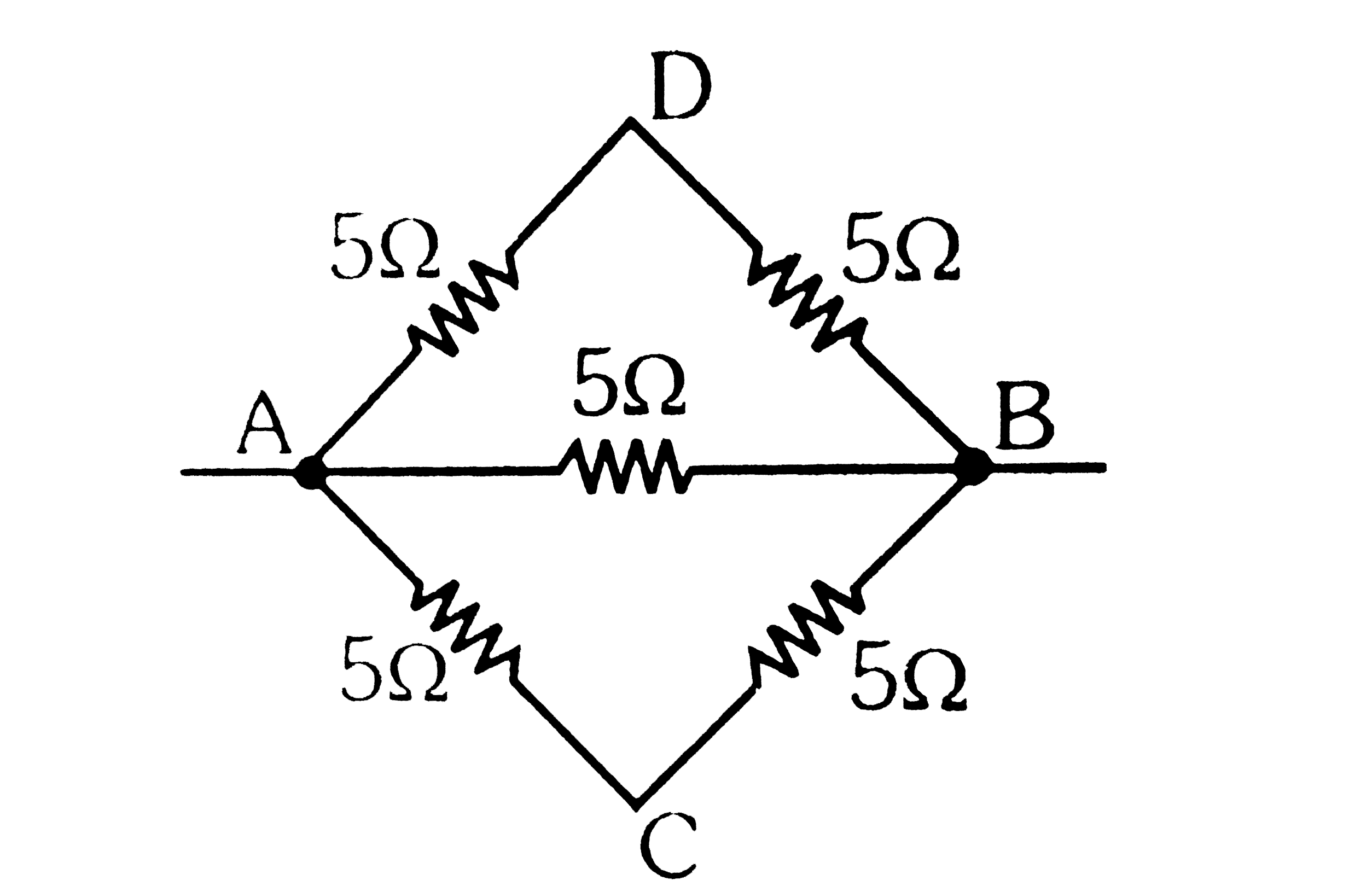
View SolutionFive resistors, each of 3 Ω, are connected as shown in Fig . Calculate the resistance
between the points P and Q,
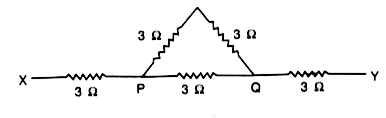
View SolutionFive resistors, each of 3 Ω, are connected as shown in Fig . Calculate the resistance
between the points X and Y.

View SolutionThe emf of a cell is ε and its internal resistance is r. its terminals are connected to a resistance R. The potential difference between the terminals is 1.6V for R=4Ω, and 1.8V for R=9Ω. Then,
View SolutionSixteen resistor, each resistane 16Ω are connected in the circuit as shown in fig. the net resistance between A and B is

View SolutionEight resistances each of resistance 5Ω are connected in the circuit as shown in figure. The equivalent resistance between A and B is
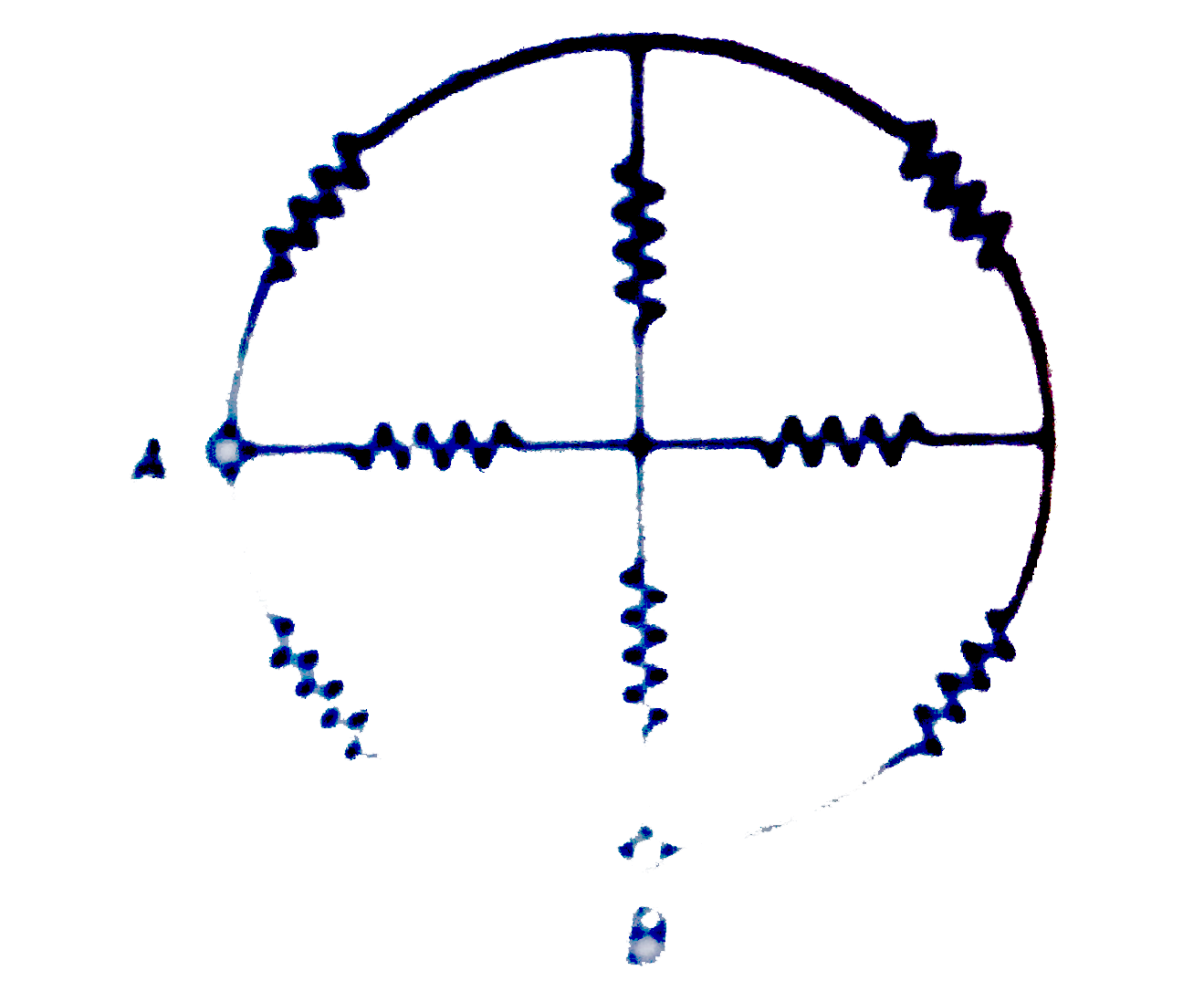
View SolutionTwelve resistors each of resistance 1Ω are connected in the circuit shown in figure. Net resistance between point A and H would be

View SolutionA metallic wire having a resistance of 20Ω is bent in order to form a complete circle. Calculate the resistance between any two diametrically opposite points on the circle.
View Solution
