Derive an expression for magnetic field induction at a point on the axial line of a short bar magnet.

Text Solution

Verified by Experts

Let 2l be the magnetic length of a bar magnet with centre O.

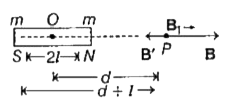
The magnetic dipole moment of the magnet is M, where $M = m \times 2 I, O P = d$ , is the distance of the point P on the axial line from the centre of the magnet.
Magnetic field at P due to N pole of magnet,
$B = \frac{μ_{0}}{4 π} \times \frac{m \times 1}{{(N P)}^{2}}$
$= \frac{μ_{0}}{4 π} \frac{m}{{(d - l)}^{2}}$ ,
along NP produced
Magnetic field at P due to S people of magnet,
$B = \frac{μ_{0}}{4 π} \times \frac{m \times 1}{{(S P)}^{2}}$
$= \frac{μ_{0}}{4 π} \frac{m}{{(d + l)}^{2}}$ ,
along PS produced.
$∴$ Magnetic field at P due to the bar magnet,
$B_{1} = B - B .$
$= \frac{μ_{0}}{4 π} \frac{m}{{(d - l)}^{2}} - \frac{μ_{0}}{4 π} \frac{m}{{(d + l)}^{2}}$
$B_{1} = \frac{μ_{0} m}{4 π} [\frac{1}{{(d - l)}^{2}} - \frac{1}{{(d + 1)}^{2}}]$
$B_{1} = \frac{μ_{0} m}{4 π} [\frac{{(d + l)}^{2} - {(d - l)}^{2}}{{(d^{2} - l^{2})}^{2}}] [\begin{matrix} ∵ (a - b) (a + b) = a^{2} - b^{2} \end{matrix}]$
$= \frac{μ_{0} m .4 l d}{4 π {(d^{2} - l^{2})}^{2}}$
$B_{1} = \frac{μ_{0}}{4 π} \frac{2 M d}{{(d^{2} - l^{2})}^{2}} [∵ M = m \times 2 l]$
When the magnet is short, $l^{2} < < d^{2}$
$∴ l^{2}$ is neglected
$∴ B_{1} = \frac{μ_{0}}{4 π} \frac{2 M d}{d^{4}}$
$\Rightarrow B = \frac{μ_{0}}{4 π} \frac{2 M}{d^{3}}$
The direction of $B_{1}$ is along NP produced.

Updated on:21/07/2023