Derive the expression for the magnetic field intensity due to a bar magnet at any point on its broadside-on position. Find the same when the length of the magnet is small.

Text Solution

Verified by Experts

Expression for the magnetic field due to a bar magnet at any point on its broadside-on-position.
In figure, the point P is shown on equatorial line of the same bar magnet, where OP = d. Magnetic field at P due to N pole of magnet,
$B = \frac{μ_{0}}{4 π} \frac{m \times 1}{{(N P)}^{2}}$
$= \frac{μ_{0}}{4 π} \frac{m}{(d^{2} + l^{2})}$
along NP produced,

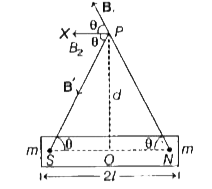
Magnetic field at P due to S pole of magnet,
$B . = \frac{μ_{0}}{4 π} \times \frac{m \times 1}{S P^{2}}$
$= \frac{μ_{0}}{4 π} \frac{m}{(d^{2} + l^{2})}$
along PS.
As B = B. in magnitude, their components $B \sin θ$ along OP produced and $B . \sin θ$ along PO canel. However, components along PX parallel to NS add. Therefore, magnetic field at P due to the bar magnet,
$B_{2} = B \cos θ + B . \cos θ = 2 B . \cos θ$ , along PX
$B_{2} = 2 \frac{μ_{0}}{4 π} \frac{m}{(d^{2} + l^{2})} \times \frac{l}{\sqrt{(d^{2} + l^{2})}} = \frac{μ_{0}}{4 π} \frac{m \times 2 l}{{(d^{2} + l^{2})}^{3 / 2}}$
$B_{2} = \frac{μ_{0}}{4 π} \frac{M}{{(d^{2} + l^{2})}^{3 / 2}}$
$∴ H = \frac{B_{2}}{μ_{0}} = \frac{1}{4 π} \frac{M}{{(d^{2} + l^{2})}^{3 / 2}}$
If the magnet is short, $l^{2} < < d^{2}$
$∴ B_{2} = \frac{μ_{0}}{4 π} \frac{M}{{(d^{2})}^{3 / 2}} = \frac{μ_{0}}{4 π} \frac{M}{d^{3}}$
implies Magnetic field intensity at point P is
$H = \frac{1}{4 π} \frac{M}{d^{3}}$

Updated on:21/07/2023

|

Class 12 PHYSICS MAGNETISM AND MATTER

Similar Questions

Knowledge Check

The magnetic field due to a bar magnet _____
Ahas the same direction at any point
Bis uniform
Cis non-uniform
Ddoes not exist

Recommended Questions

Home
Ask Doubt
Profile