State Biot-Savart.s law. Derive an expression for magnetic field at a point near an infinitely long and straight current carrying conductor.

Text Solution

Verified by Experts

Biot-Savart.s law states that the magnetic field at any point P at a distance r from a current carrying element is directly proportional to the current element (Idl) $sin θ$ and inversely proportional to the square of distance between point P and current element.

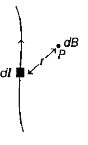
i.e. $d B \propto I d l sin θ and d B \propto \frac{1}{r^{2}}$
$\Rightarrow d B \propto \frac{I d l sin θ}{r^{2}}$
$\Rightarrow d B = \frac{μ_{0}}{4 π} . \frac{I d l sin θ}{r^{2}}$
Magnetic field due to infinite straight current carrying conductor
Consider a straight conductor XY carrying current I. We wish to find magnetic field at point P whose perpendicular distance from the wire is $P Q = a$ .
Consider a small current element dl of the conductor at point O. Its distance from Q is $O Q = l$ .
Let r be the position vector of point P relative to the current element and $θ$ be the angle between dl and r.
Now according to Biot-Savart.s law,
$d B = \frac{μ_{0}}{4 π} . \frac{I d l sin θ}{r^{2}}$

From right $Δ O Q P, θ + ϕ = 90^{\circ}$
$\Rightarrow θ = 90^{\circ} - ϕ$
$sin θ = sin (90^{\circ} - ϕ) = cos ϕ$
$cos ϕ = \frac{α}{r}$
$\Rightarrow r = \frac{α}{cos ϕ} = α sec ϕ$
$tan ϕ = \frac{l}{α} \Rightarrow l = a tan ϕ$
On differentiating, we get $d l = a {sec}^{2} ϕ d ϕ$
$d B = \frac{μ_{0}}{4 π} \frac{I (α {sec}^{2} ϕ d ϕ) cos ϕ}{α^{2} {sec}^{2} ϕ}$
$\Rightarrow d B = \frac{μ_{0} I}{4 π α} cos ϕ d ϕ$
On integrating above relation within the limits - $ϕ_{1} and ϕ_{2}$
$B = \int_{- ϕ_{1}}^{ϕ_{2}} d B = \frac{μ_{0} I}{4 π α} \int_{- ϕ_{1}}^{ϕ_{2}} cos ϕ d ϕ$
$= \frac{μ_{0} I}{4 π α} {(sin ϕ)}_{- ϕ_{1}}^{ϕ_{2}}$
$= \frac{μ_{0} I}{4 π α} ({sin α}_{2} + {sin ϕ}_{1})$

Updated on:21/07/2023

|

Class 12 PHYSICS VERY SIMILAR TEST 1

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile