State Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor . Solution in Kannada
The integral of the products of tangential component of magnetic field and the element of length in a closed loop is equal to μ0 times the total current passing through the surface.
∮→B.D→l=μ0I
Let I be the current in the wire PQ . Let P be a point at a perpendicular distance r from the wire . Let dl be the element of length of the closed path. The direction of the magnetic field will be tangential to the point P on the element .
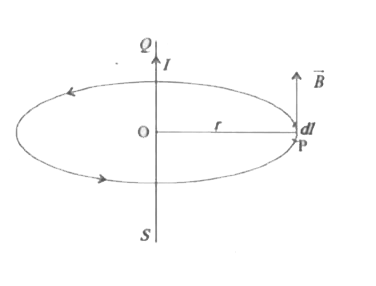
Applying Ampere.s circuital law , we have
∮→B.d→l=μ0I
i.e., ∮Bdlcos0∘=μ0I
θ=0∘ between tangent drawn at P to the element of length dl and →B.
Thus , B∮dl=μ0I
or B=μ0I∮dl=μ0I2πr
Thus , B∝1r
Topper's Solved these Questions
- ANNUAL EXAM QUESTION PAPER -MARCH -2017 BOOK - SUBHASH PUBLICATIONCHAPTER - ANNUAL EXAM QUESTION PAPER -MARCH -2017 EXERCISE - PART -D
12 Videos
- ANNUAL EXAMINATION QUESTION PAPER (WITH ANSWER) MARCH 2018BOOK - SUBHASH PUBLICATIONCHAPTER - ANNUAL EXAMINATION QUESTION PAPER (WITH ANSWER) MARCH 2018EXERCISE - Part-C
11 Videos
Similar Questions
Deduce the condition for balance of a wheatstone's bridge using Kirchoffs rules .
View SolutionMention any three properties of an electric charge.
View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic induction at a point near an infinitely long straight conductor carrying an electric current.
View SolutionObtain an expression for the magnetic field at a point due to an infinitely long thin conductor or wire by applying Ampere's circuital law.
View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
View SolutionUsing Ampere.s circuital law derive an expression for magnetic field due to infinitely long current carrying wire at a point at distance Yfrom it.
View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
View SolutionState Ampere's circuital law . Using it, derive the expression for magnetic field at a point due to a long current carrying conductor .
View SolutionState Biot-Savart.s law. Derive an expression for magnetic field at a point near an infinitely long and straight current carrying conductor.
View SolutionState Ampere's circuital law. Derive an expression for magnetic field due to long solenoid .
View SolutionState Ampere's circuital law. By using it derive an expression for magnetic field intensity at a point due to a straight current carrying conductor.
View SolutionUsing Ampere's circuital law, derive an expression for the magnetic field along the axis of a toroidal solenoid.
View SolutionUsing Ampere's circuital theorem, calculate the magnetic field due to an infinitely long wire carrying current I.
View Solution
