The median salary of 100 employees of a factory is ₹ 24.800, whose frequency distribution is given below. Find the missing frequencies f1andf2
Salary (in ₹) Number of employees 10000−15000 1815000−20000 f120000−25000 f225000−30000 1530000−35000 1235000−40000 22
The correct Answer is:f1=8,f2=25
Topper's Solved these Questions
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - Objective Questions (Fill in the blanks)
5 Videos
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - Objective Questions (MCQ.s)
10 Videos
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - Test your Skills
18 Videos
- SOME AAPLICATIONS OF TRIGONOMETRYBOOK - KUMAR PRAKASHANCHAPTER - SOME AAPLICATIONS OF TRIGONOMETRYEXERCISE - Objective Questions
24 Videos
- SURFACE AREAS AND VOLUMESBOOK - KUMAR PRAKASHANCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - TEST YOUR SKILLS
5 Videos
Similar Questions
Knowledge Check
The frequency distribution for x is an given below. What is the range of f? <br>{:(x,f),(0,1),(1,5),(2,4),(3,4):}
A0B1C3D4
The mean of the following frequency distribution is 57.6 and the sum of the observations is 50. Find the missing frquencies f1andf2 :

View SolutionThe mean of the following frequency distribution is 57.6 and the number of observation is 50. Find the missing frequency f1&f2
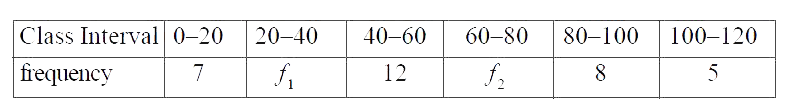
View SolutionThe mean of the following distribution is 62.8 and the sum of all the frequencies is 50. Find the missing frequencies f1 and f2

View SolutionThe total number of observations in the following distribution table is 120 and their mean is 50. Find the value of missing frequencies f1andf2 :

View SolutionThe total number of observations in the following distribution table is 120 and their mean is 50. Find the value of missing frequencies f1andf2 :

View SolutionThe total number of observations in the following distribution tale is 120 and their mean is 50. Find the values of missing frequencies f1 and f2
View SolutionThe mean of the following frequency distribution is 62.8 and the sum of all frequencies is 50. Compute the missing frequencies f1 and f2:
View Solution

