In a triangle ABC, points D and E are on segments BC and AC such that BD= 3DC and AE= 4EC. Point P is on line ED such that D is the midpoint of segment EP. Lines AP and BC intersect at point S, Find the ratio BS/SD
Text Solution
The correct Answer is:7/2
|
Topper's Solved these Questions
- GEOMETRYBOOK - RESONANCECHAPTER - GEOMETRYEXERCISE - Exercise-1 (Part-I: Previous Asked Question For Pre RMO)
50 Videos
- FUNDAMENTAL OF MATHEMATICSBOOK - RESONANCECHAPTER - FUNDAMENTAL OF MATHEMATICSEXERCISE - Exercise
138 Videos
- INDEFINITE INTEGRATION BOOK - RESONANCECHAPTER - INDEFINITE INTEGRATION EXERCISE - SELF PRACTIC PROBLEMS
25 Videos
Similar Questions
Knowledge Check
For a triangle ABC,D and E are two points on AB and AC such that AD=14AB,AE=14AC. If BC=12cm, then DE is
Aa) 5 cmBb) 4 cmCc) 3 cmDd) 6 cmIn ΔABC,∠B=90∘. If points D and E are on side BC such that BD=DE=EC, then which is true?
AAE2=5AC2+3AD2B5AE2=2AC2+3AD2C8AE2=3AC2+5AD2D5AE2=3AC2+2AD2For a triangle ABC,D and E are two points on AB and AC such that AD=14AB,AE=14AC. If BC=12cm, then DE is
A5 cmB4 cmC3 cmD6 cm
In triangle ABC, D is a point in side AB such that AB = 4AD and E is a point in AC such that AC = 4AE. Show that BC : DE = 4:1
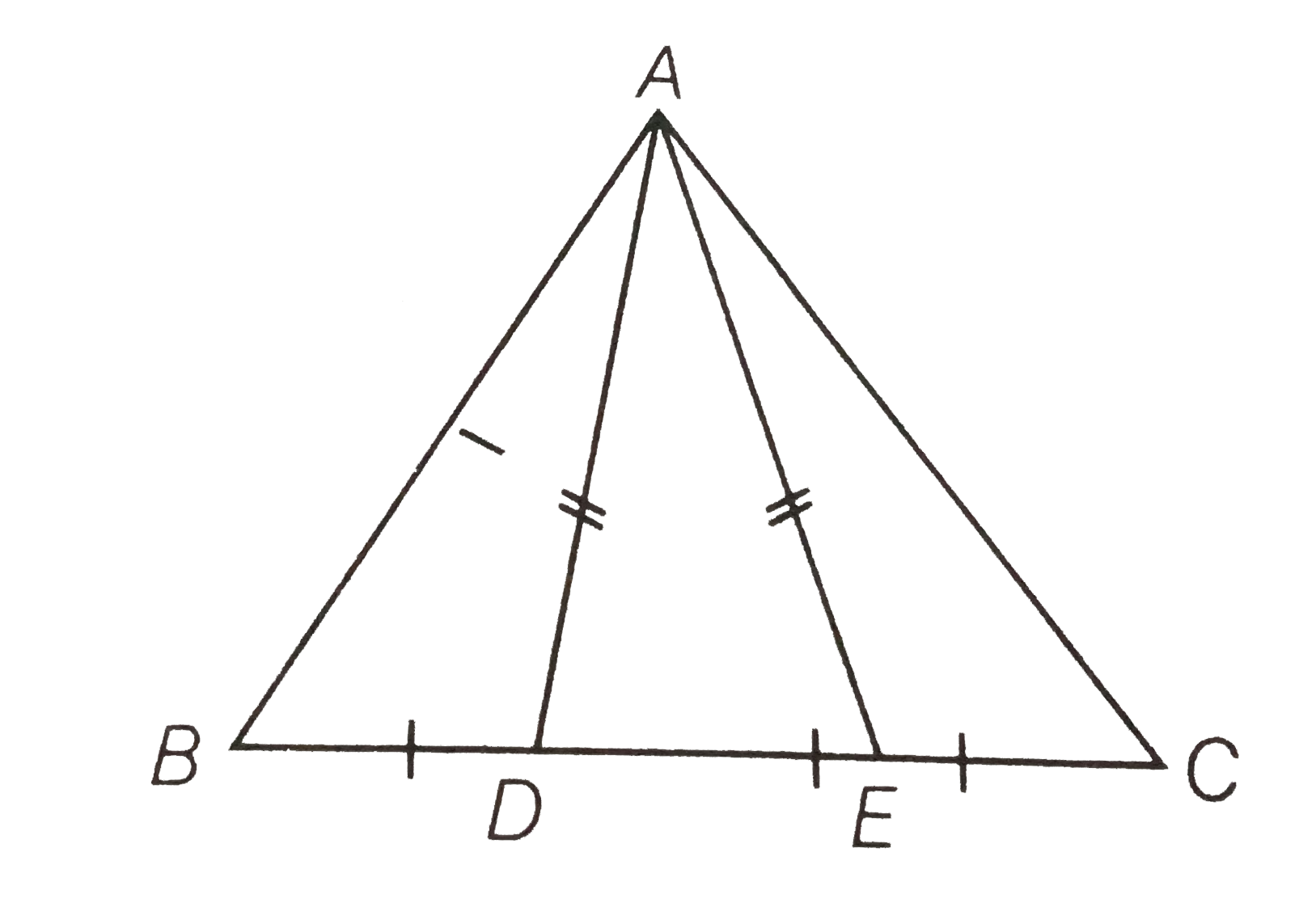
View SolutionIn figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE. Show that ΔABD≅ΔACE.
View SolutionIn a triangle ABC, if a=5,b=4andc=3,DandE are the points on BC such that BD=DE=EC. If ΔDAE=θ, then tanθ=
View SolutionIn figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE.Show that ΔABD≅ΔACE.

View SolutionIn a triangle ABC, a point D is chosen on BC such that BD : DC = 2 : 5. Let P be a point on the circumcircleABC such that ∠PDB=∠BAC. Then PD : PC is :-
View Solution