ABCD is a square and AB=1. Equilateral triangle AYB and CXD are drawn such that X and Y are inside the square. What is the length of XY?
Text Solution
The correct Answer is:√3−1
|
Topper's Solved these Questions
- GEOMETRYBOOK - RESONANCECHAPTER - GEOMETRYEXERCISE - Exercise-1 (Part-I: Previous Asked Question For Pre RMO)
50 Videos
- FUNDAMENTAL OF MATHEMATICSBOOK - RESONANCECHAPTER - FUNDAMENTAL OF MATHEMATICSEXERCISE - Exercise
138 Videos
- INDEFINITE INTEGRATION BOOK - RESONANCECHAPTER - INDEFINITE INTEGRATION EXERCISE - SELF PRACTIC PROBLEMS
25 Videos
Similar Questions
Knowledge Check
ABCD is a square and ABE is an equilateral triangle outside the square then
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of theseABCD is a square and AOB is an equilateral triangle. What is the value of ∠DOC?
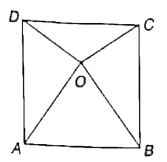 A120∘B150∘C125∘Dcan't be determined
A120∘B150∘C125∘Dcan't be determinedA square and an equilateral triangle are drawn on the same base. The ratio of their area is
A2:1B1:1C√3:4D4:√3
ABCD is square and CDE is an equilateral triangle outside the square. What is the value (in degrees) of ∠BEC?
View SolutionABCD is a square, and ABE is an equilateral triangle. ACandEB are produced to meet at F. Calculate the angles of ΔABF.
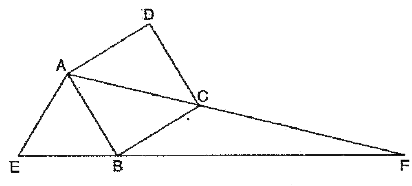
View SolutionIn the given figure,ΔCDE is an equlatel triangle triangle formed on a side CD of a square ABCD.Show that ΔADE≅ΔBCE.
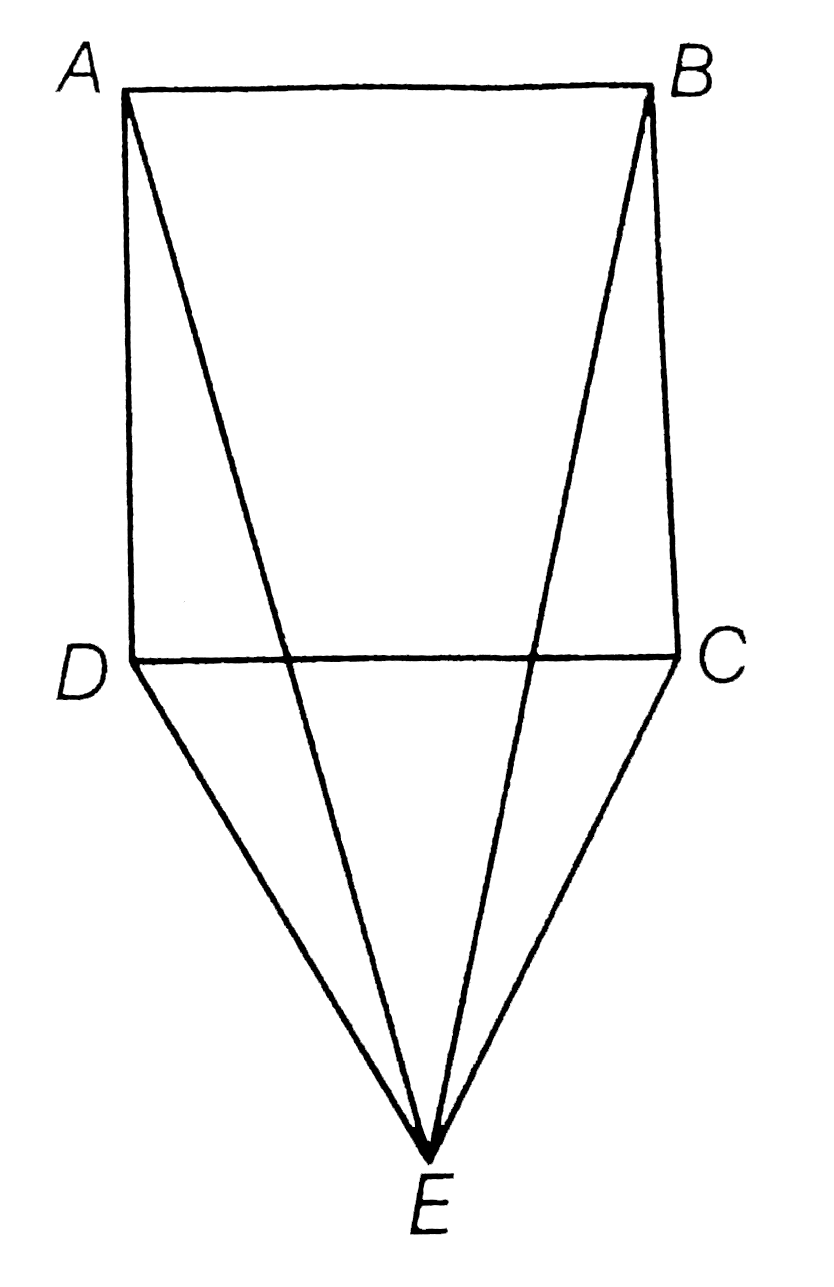
View SolutionABCD is square and CDE is an equilateral triangle outside the square. What is the value (in degrees) of ∠BEC?
View SolutionABCD is square and CDE is an equilateral triangle outside the square. What is the value (in degrees) of ∠BEC ?
View Solution
